Question

A particle moves on a circle of radius $r$ with centripetal acceleration as a function of time as ${a_c} = {k^2}r{t^2}$ where $k$ is a positive constant. Find the following quantities as a function of time at an instant.
a. The speed of the particle
b. The tangential acceleration of the particle
c. The resultant acceleration, and
d. Angle made by the resultant with tangential direction.

Answer 1

Hint: Equate the centripetal acceleration at a radius to the given function of time. This way find a relation between velocities at a particular instant. Use this relation to calculate all other quantities.

Complete answer:

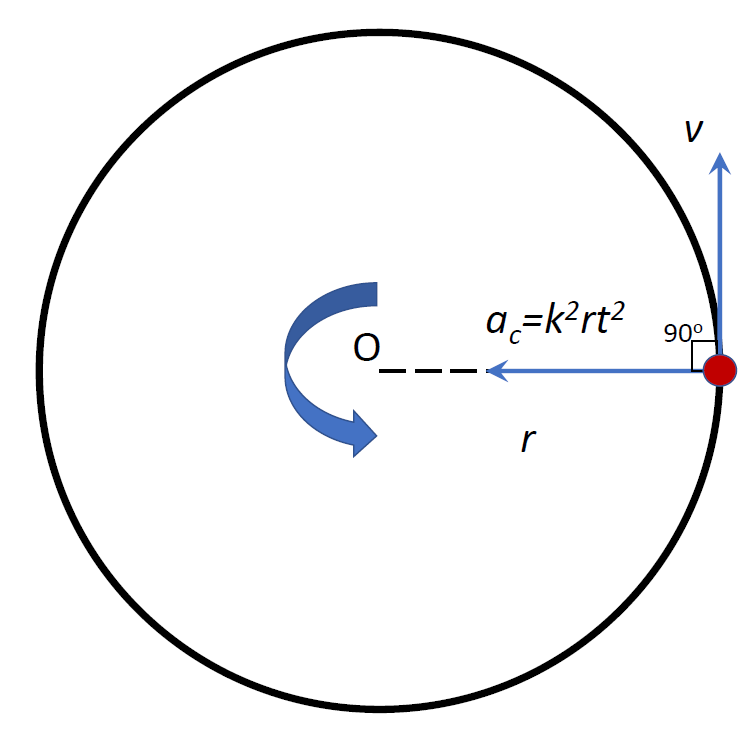
A particle is moving on a circle of radius r as shown in the above diagram with the centripetal acceleration as follows:
${a_c} = {k^2}r{t^2}$ where $k$ is a constant. Now we already know an expression for centripetal acceleration which is ${a_c} = \dfrac{{{v^2}}}{r}$. Equating these two expressions, as both are centripetal acceleration at radius r, we get:
$\dfrac{{{v^2}}}{r} = {k^2}r{t^2}$
$\Rightarrow {v^2} = {k^2}{r^2}{t^2}$
$\Rightarrow v = krt$
Here, the particle is moving around a circle of radius $r$ with velocity $v$. When we say velocity its direction is changing along the circular path. This change of direction is centripetal acceleration. But the magnitude as per above expression is changing with time which is the speed of the particle at a particular instant. Thus answering the first question.
In the second question, we are asked to find the tangential acceleration, which could be defined as the derivative the above expression as the speed is changing with respect to time along the circular path which will result into non-zero tangential acceleration as the direction of velocity at that instant is tangential. So taking derivative of the above expression of velocity we get the tangential acceleration as follows:
${a_T} = \dfrac{{dv}}{{dt}} = kr\dfrac{{dt}}{{dt}} = kr$
Resultant acceleration at any instant is given as follows from vector addition:
${a_R} = \sqrt {a_c^2 + a_T^2 + 2{a_c}{a_T}\cos \theta } = \sqrt {a_c^2 + a_T^2} $
Angle between both the acceleration is 90 degrees as one, centripetal acceleration is directed inward towards the centre of the circular path and second, the tangential acceleration as by the name, acts in the tangential direction perpendicular to the radius of the circle. Thus the magnitude is as follows:
${a_R} = \sqrt {{{({k^2}r{t^2})}^2} + {{(kr)}^2}} = kr\sqrt {{k^2}r{t^2} + 1} $ and therefore answering the third question.
In the last question, we are asked to find the angle that resultant makes with the tangential direction. Consider the angle as $\phi $ and it can be given as follows:
$\tan \phi = \dfrac{{{a_c}}}{{{a_T} + {a_c}\cos \theta }} = \dfrac{{{k^2}r{t^2}}}{{kr + {k^2}r{t^2}\cos (90)}} = \dfrac{{{k^2}r{t^2}}}{{kr}} = k{t^2}$. Therefore, $\phi = {\tan ^{ - 1}}(k{t^2})$.
Since the individual vectors are perpendicular to each other, that is why we have this simple expression of tangent term. If the vectors had not been perpendicular then one more term would be present in the denominator which will be a component of ${a_c}$ in the direction of ${a_T}$.

Note: Here we consider the radius of the circle as constant. If the radius was not constant, then the derivative step above will have more terms. Be careful while working with the variable with different power and in fraction form.