Question

When a particle moves in a circle with uniform speed, then:
(A) its velocity and acceleration both are constant
(B) its velocity is constant but the acceleration changes
(C) its acceleration is constant but velocity changes
(D) its velocity and acceleration both change

Answer 1

Hint: A particle moving in a circle exhibits a circular motion. To comment whether the velocity and acceleration of the particle is changing or is constant, we need to understand what types of terms are these two. Velocity and acceleration are vector quantities. So, a change in either the magnitude or direction will bring about a change in these quantities. We shall use this fact to answer our question.

Complete answer:
Let us first denote some terms that we are going to use in our solution. Let the velocity of the particle be ‘$\overrightarrow{v}$ ’, then it has been given that the magnitude of this velocity vector is constant. This result is established by the fact that the speed of the particle is uniform. Also, let the acceleration of the particle be denoted by ‘$\overrightarrow{a}$’.
Let us examine this case of a particle moving in a circular motion with the help of a diagram and see if any changes occur in the particle’s motion in a very small-time duration. This diagram is represented below as follows:

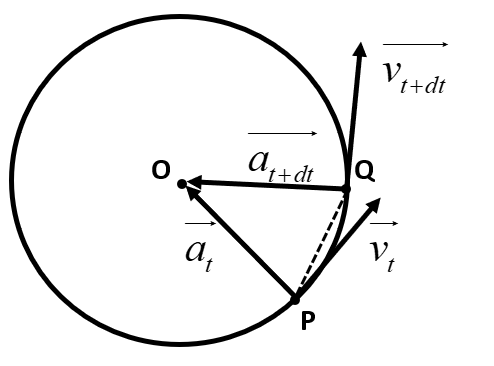
From the above diagram we can see that over a small distance PQ, the direction of velocity vector and the acceleration vector changes. This implies the fact that both velocity and acceleration of the particle changes in a circular motion.
Hence, its velocity and acceleration both change.

Hence, option (D) is the correct option.

Note:
A body travelling in a circular motion with uniform speed has its acceleration vector always pointed towards the center of the circular motion. And if the speed of the particle is non-uniform, then it acquires a tangential acceleration which changes the direction of acceleration from “towards center” to “depends upon the vector result of tangential and centripetal acceleration”.