Question

A particle is projected with an angle of projection to the horizontal line passing through the points (P,Q) and (Q,P) referred to horizontal and vertical axes (can be treated as X-axis and Y-axis respectively). The angle of projection can be given by
A. ${{\tan }^{-1}}[\dfrac{{{P}^{2}}+{{Q}^{2}}+PQ}{PQ}]$
B. ${{\tan }^{-1}}[\dfrac{{{P}^{2}}+{{Q}^{2}}-PQ}{PQ}]$
C. ${{\tan }^{-1}}[\dfrac{{{P}^{2}}+{{Q}^{2}}}{2PQ}]$
D. ${{\tan }^{-1}}[\dfrac{{{P}^{2}}+{{Q}^{2}}+PQ}{2PQ}]$

Answer 1

Hint: Use the equation of path of a projection. Do not consider points of projection. The angle made by the velocity of the projection with the horizontal. The path followed by the projection in space is called its trajectory.

Complete Step-by-Step solution:
Projection: An object thrown in the air with initial velocity in any direction, making some angle with the horizontal, moving freely under the action of gravity is called projection.
First understand what the question wants to convey.
Let’s take a particle and project it with an angle of $\theta $ to the horizontal line. This particle is passing through (P, Q) and (Q, P), which can be referred to as the horizontal x-axis and vertical as y – axis.
Aim: Find angle of projection.
Diagram:

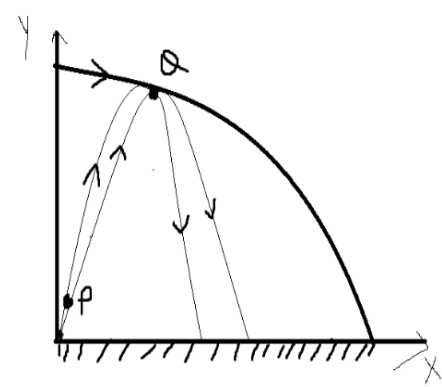
We know that equation of trajectory of projectile motion is given by,
$y=x\tan \alpha [1-\dfrac{x}{R}]$
where,
x & y = horizontal and vertical axis
R = range of particles up to which particle will travel.
$\alpha $= Angle of projection which is always measured from the horizontal axis.
Consider y as Q and x as P.

Now solve for P then for Q.
For Q:
$Q=P\tan \theta [1-\dfrac{P}{R}]$

Similarly, for P,
$P=Q\tan \theta [1-\dfrac{Q}{R}]$

Divide equation Q by P
We get,
( tan $\theta $ will get cancelled)
\[\begin{align}
  & \Rightarrow \dfrac{Q}{P}=\dfrac{P}{Q}\dfrac{[1-\dfrac{P}{R}]}{[1-\dfrac{Q}{R}]} \\
 & \Rightarrow \dfrac{{{Q}^{2}}}{{{P}^{2}}}=\dfrac{R-P}{R-Q} \\
 & \Rightarrow {{Q}^{2}}R-{{Q}^{3}}=R{{P}^{2}}-{{P}^{3}} \\
 & \Rightarrow {{P}^{3}}-{{Q}^{3}}=R({{P}^{2}}-{{Q}^{2}}) \\
\end{align}\]
We know the expansion as
${{P}^{3}}-{{Q}^{3}}=(P-Q)({{P}^{2}}+{{Q}^{2}}+PQ)$
Put value back we get,
$\begin{align}
  & \Rightarrow (P-Q)({{P}^{2}}+{{Q}^{2}}+PQ)=R(P-Q)(P+Q) \\
 & \Rightarrow R=\dfrac{({{P}^{2}}+{{Q}^{2}}+PQ)}{(P+Q)} \\
\end{align}$
Put value of R in equation of P
We get,
$\begin{align}
  & \Rightarrow \dfrac{P}{Q}=\tan \theta [\dfrac{{{P}^{2}}+{{Q}^{2}}+PQ-QP-{{Q}^{2}}}{{{P}^{2}}+{{Q}^{2}}+PQ}] \\
 & \Rightarrow \tan \theta =\dfrac{P}{Q}[\dfrac{{{P}^{2}}+{{Q}^{2}}+PQ}{{{P}^{2}}}] \\
 & \Rightarrow \theta ={{\tan }^{-1}}[\dfrac{{{P}^{2}}+{{Q}^{2}}+PQ}{PQ}] \\
\end{align}$
Correct option is (A).

Note: Projectile moves with constant acceleration due to gravity which is acting in vertically downward direction. Careful while solving the equation part. Choose options carefully because mistakes in + and – signs can make our answer wrong.