Question

A particle is moving with constant speed v in circle. What is the magnitude of average velocity after half rotation?
A. 2v
B. $2\dfrac{v}{\pi}$
C. $\dfrac{v}{2}$
D. $\dfrac{v}{2\pi}$

Answer 1

Hint: We need to find the time taken to cover the distance and then we need to find displacement covered by the particle. And from these, we will get the average velocity of the particle using the velocity formula.

Complete step by step solution:
Let us consider the circular path of radius R and a particle is travelling on the path with the given velocity v. We can illustrate the given conditions as follows,

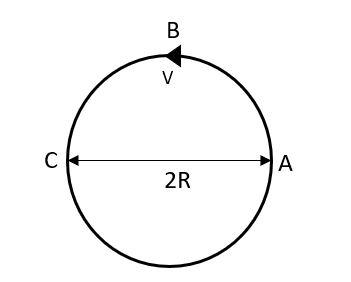
It has been given that the particle has covered half rotation. So, let us assume that the particle is initially at A and travels through the path ABC, thus distance covered by the particle is $\pi R$ with a velocity v. So, time taken, $t=\dfrac{\pi R}{v}$.
Now, we need to find out the average velocity of the particle, which is given by $\dfrac{\text{displacement}}{\text{time taken}}$.
Here, total displacement will be equal to the diameter, that is 2R.
So, average velocity$=\dfrac{2R}{\dfrac{\pi R}{v}}=v\dfrac{2}{\pi}$.
Hence, option d is the correct answer.

Note: We should be careful while considering the velocity and speed. In this question, it has been given to find out the average velocity while in the question, distance and speed is given. So, in order to find the average velocity, we need to find the displacement covered. Although, we can also make a minor mistake in considering the angular velocity by converting the velocity given.