Question

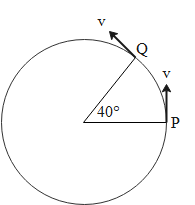
A particle is moving in a circle of radius r with a constant speed v. The change in velocity in moving from P to Q is

$
  {\text{A}}{\text{. 2v cos 20}}^\circ \\
  {\text{B}}{\text{. 2v sin 20}}^\circ \\
  {\text{C}}{\text{. 2v cos 40}}^\circ \\
  {\text{D}}{\text{. 2v sin 40}}^\circ \\
$

Answer 1

Hint: If we consider the particle to be moving in an x-y plane, then we can resolve the components of the velocity along the x-axis and y axis. Change in velocity is equal to difference between velocity at Q and the velocity at P.

Detailed step by step answer:
We are given a particle which is moving in a circle of radius r with a constant speed v. The diagram shows two points of the trajectory of the particle.

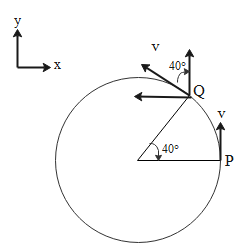
If we consider the particle is moving in a x-y plane then at point P, the expression for velocity can be written as follows since it's pointing towards the y-axis.

$\overrightarrow {{V_P}} = V\widehat j$

For point Q, we must write the velocity vector in terms of its components as follows:

$\overrightarrow {{V_Q}} = - V\sin 40^\circ \widehat i + V\cos 40^\circ \widehat j$

Here the angle at Q has been calculated using the fact that a tangent to a circle subtends a right angle with the radius of the circle.

Now the change in velocity from P to Q can be given as

$
  \overrightarrow {\Delta V} = \overrightarrow {{V_Q}} - \overrightarrow {{V_P}} \\
   = - V\sin 40^\circ \widehat i + \left( {V\cos 40^\circ - V} \right)\widehat j \\
   = - V\sin 40^\circ \widehat i + V\left( {\cos 40^\circ - 1} \right)\widehat j \\
$

Now we need to calculate the magnitude of this change in velocity which will give us the required answer.

$
  \Delta V = |\overrightarrow {\Delta V} | = \sqrt {{{\left( { - V\sin 40^\circ } \right)}^2} + {{\left\{ {V\left( {\cos 40^\circ - 1} \right)} \right\}}^2}} \\
   = V\sqrt {{{\sin }^2}40^\circ + {{\left( {\cos 40^\circ - 1} \right)}^2}} \\
   = V\sqrt {{{\sin }^2}40^\circ + {{\cos }^2}40^\circ + 1 - 2\cos 40^\circ } \\
$

Using the identity: ${\sin ^2}\theta + {\cos ^2}\theta = 1$

$
  \Delta V = V\sqrt {2 - 2\cos 40^\circ } \\
   = V\sqrt {2\left( {1 - \cos 40^\circ } \right)} \\
$

Using the identity: $1 - \cos \theta = {\sin ^2}\dfrac{\theta }{2}$

$
  \Delta V = V\sqrt {4{{\sin }^2}20^\circ } \\
   = 2V\sin 20^\circ \\
$

This is the required change in velocity; hence, the correct answer is option B.

Note: It is mentioned that the particle is moving with constant speed. It means that the magnitude of velocity is constant but when a particle moves in a circular orbit, its speed may remain constant but the direction of velocity changes at every point of the path. Velocity changes as it is a vector quantity and it is dependent on the direction of the vector.