Question

A particle is moving along a straight line such that the square of its velocity varies with time as shown in figure. What is the acceleration of the particle at $t=4s$?

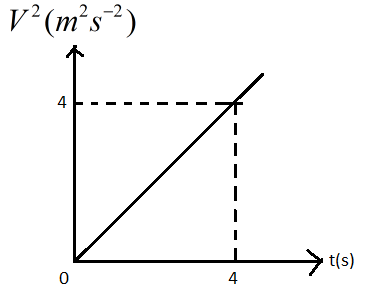
A. $4m{{s}^{-2}}$
B. $\dfrac{1}{4}m{{s}^{-2}}$
C. $\dfrac{1}{2}m{{s}^{-2}}$
D. $0$

Answer 1

Hint: The question involves the concept of gradient of the graph. The gradient of the velocity time graph gives the acceleration at any time $t$.
First form the equation of velocity and time from the graph shown above. The differentiation of velocity with time is actually acceleration.
We will get the relation of acceleration with time. Then putting the value of time given in question ,we can find the value of acceleration at that time.

Complete step-by-step answer:
From looking at the figure we can see that varies with time as a straight line means the graph has a constant slope throughout the time.
The value of slope of the curve for the velocity time equation can be found out using the coordinates given in the question.
So the straight line equation of the graph will be
${{v}^{2}}=mt$
where$m$will be a slope .
Value of $m=\dfrac{4-0}{4-0}$
$m=1$
So the straight line equation becomes ${{v}^{2}}=t$
$v=\sqrt[2]{t}..........\left( 1 \right)$
 Now for acceleration we will differentiate the equation,
$\Rightarrow {{v}^{2}}=t$
$\Rightarrow 2v\dfrac{\partial v}{\partial t}=1$
$\Rightarrow \dfrac{\partial v}{\partial t}=a=\dfrac{1}{2v}$
Putting the value of v from$\left( 1 \right)$,
$\Rightarrow a=\dfrac{1}{2\sqrt[{}]{t}}$
We have to find acceleration at time $t=4s$
$a=\dfrac{1}{2\sqrt{4}}$
$a=\dfrac{1}{4}m{{s}^{-2}}$
Hence the correct option will be B.

So, the correct answer is “Option B”.

Note: The quantity represented on the horizontal axis of the graph is independent variable and the quantity on vertical axis is the dependent variable.
In our case time is independent and velocity is a dependent variable.
Also one important point to note is that for velocity versus time graphs, the area bounded by the line and the axes represents the displacement.
Similarly the area bounded by the acceleration time graph represents velocity.