Question

A particle describes a horizontal circle in a conical funnel whose inner surface is smooth with speed of $ 0.5m{s^{ - 1}} $ . What is the height of the plane of the circle from the vertex of the funnel?
A. $ 0.25m $
B. $ 2cm $
C. $ 4cm $
D. $ 2.5cm $

Answer 1

Hint : The particle is moving in a circular path so centripetal force will act on it along with the gravitational pull. Equate both the components of force along the horizontal and vertical to find the height of the plane from the vertex of the funnel. The horizontal component of force will be, $ N\cos \theta = \dfrac{{m{v^2}}}{r} $ , the vertical component of force will be, $ N\sin \theta = mg $ . Where, $ m $ is the mass of the particle, $ N $ is the normal force acting on the particle, $ \dfrac{{m{v^2}}}{r} $ is the centripetal force, $ g $ is the gravitational acceleration.

Complete Step By Step Answer:
Here the particle is moving in a circle plane. So, the forces on the particle will be a centripetal force and the gravitational pull. Now, in equilibrium condition the net forces on the particle will be zero. Hence, we can equate all the components of the forces.

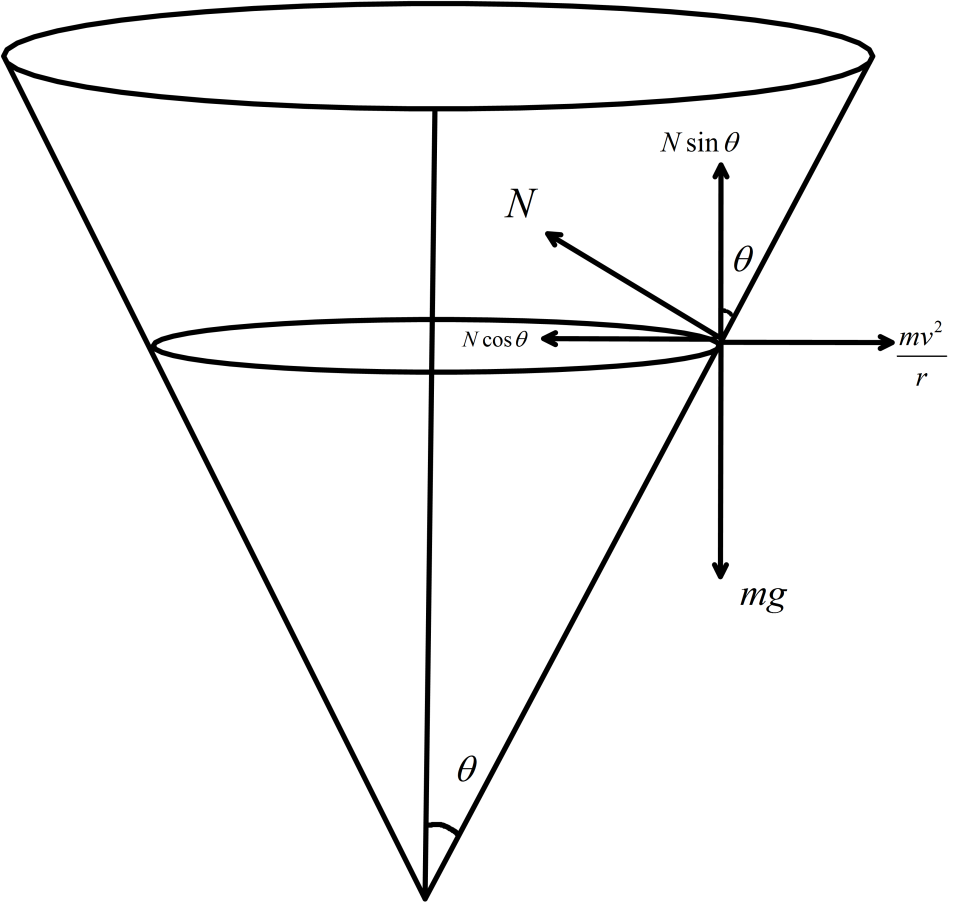
So, we can write for the horizontal component of force as, $ N\cos \theta = \dfrac{{m{v^2}}}{r} $ .…….(i)
Where, $ N $ is the normal force acting on the particle due to the plane of the cone, $ \dfrac{{m{v^2}}}{r} $ is the centripetal force acting on the particle. $ v $ is the speed of the force in the circular path and is the radius of the circular path.
And, the vertical component of force as, $ N\sin \theta = mg $ …….(ii)
Now, for a cone we can write, $ \dfrac{r}{h} = \tan \theta $ where $ h $ is the height of the plane from the vertex.
Now, from equation (i) and equation (ii) we can write,
 $ \dfrac{{N\sin \theta }}{{N\cos \theta }} = \dfrac{{mg}}{{\dfrac{{m{v^2}}}{r}}} $
Up on simplifying we get,
 $ \tan \theta = \dfrac{{gr}}{{{v^2}}} $
So, equating both the tangent we get,
 $ \dfrac{r}{h} = \dfrac{{gr}}{{{v^2}}} $
Or, $ h = \dfrac{{{v^2}}}{g} $
Here, we have given the velocity of the particle, $ v = 0.5m{s^{ - 1}} $ and gravitational acceleration is $ g = 9.8m{s^{ - 2}} $ .
So, putting these values we get,
 $ h = \dfrac{{{{0.5}^2}}}{{9.8}}m $
Or, $ h = 0.025m $
So, the height of the plane is $ h = 0.025m = 2.5cm $ .
So, option (D) is the correct answer.

Note :
The particle is kept on the circular path by the normal force of the plane. To keep a particle moving in a circular path some force like gravitation or tension must exist to cancel out the effect of the centripetal force.