Question

A particle begins at the origin and moves 1 unit to the right and reaches ${{p}_{1}}$,$\dfrac{1}{2}$ unit up and reaches ${{p}_{2}}$ , $\dfrac{1}{4}$ unit to the right and reaches ${{p}_{3}}$, $\dfrac{1}{8}$ unit down and reaches ${{p}_{4}}$. $\dfrac{1}{16}$ unit to the right and reaches ${{p}_{5}}$ and so on. If the co-ordinates of ${{p}_{n}}$ are $\left( {{x}_{n}},{{y}_{n}} \right)$ find $\underset{n\to \infty }{\mathop{\lim }}\,{{p}_{n}}$. \[\]
A. $\left( 2,3 \right)$\[\]
B. $\left( \dfrac{4}{3},\dfrac{2}{5} \right)$\[\]
C. $\left( \dfrac{2}{5},1 \right)$\[\]
D. $\left( \dfrac{4}{3},\dfrac{5}{2} \right)$\[\]

Answer 1

Hint: We firs find the coordinates of the points ${{p}_{1}},{{p}_{2}},{{p}_{3}},{{p}_{4}},{{p}_{5}},...$. We find that the $x-$coordinate ${{x}_{n}}$and $y-$coordinate ${{y}_{n}}$of the point ${{p}_{n}}$ are the sum of first $n$ terms of infinite GP sequences . We use the fact that the sum ${{x}_{1}}+{{x}_{2}}+{{x}_{3}}...$ is equal to $\underset{n\to \infty }{\mathop{\lim }}\,{{x}_{n}}$ and the limit will sum of the infinite GP series. We find $\underset{n\to \infty }{\mathop{\lim }}\,{{x}_{n}},\underset{n\to \infty }{\mathop{\lim }}\,{{y}_{n}}$ and then $\underset{n\to \infty }{\mathop{\lim }}\,{{p}_{n}}$. \[\]

Complete step by step answer:
We know that ${{x}_{1}}+{{x}_{2}}+{{x}_{3}}...=\underset{n\to \infty }{\mathop{\lim }}\,{{x}_{n}}$ provided the sequence $\left( {{x}_{n}} \right)$ is convergent. We also know that a geometric progression (GP ) series is the sum of terms in a geometric sequence $a,ar,a{{r}^{2}},...$ where $a$ is the first term and $r$ is the common ratio between two consecutive terms . The sum of first $n$ terms is given by
\[S=a+ar+a{{r}^{2}}+...+a{{r}^{n-1}}=\dfrac{a\left( {{r}^{n}}-1 \right)}{r-1}\]
The sum of a GP series with infinite terms and condition $\left| r \right|<1$ is given by,
\[S=\dfrac{a}{1-r}\]

We are given in the question that the particle begin from the origin whose co-ordinate is $O\left( 0,0 \right)$. It moves 1 unit to the right and reaches ${{p}_{1}}$. Now the distance of ${{p}_{1}}$ from $y-$axis is 1 unit which is the abscissa of its co-ordinate and it has not moved above $x-$axis . So the co-ordinate is ${{p}_{1}}\left( 1,0 \right)$. Similarly we move to the points ${{p}_{2}},{{p}_{3}},{{p}_{4}},{{p}_{5}},...$ and find their co-ordinates as shown in the following figure. \[\]

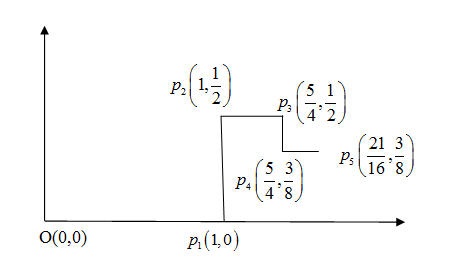
We can see from the figure when we move from ${{p}_{1}}$ to ${{p}_{2}}$ as given in the question by a distance of $\dfrac{1}{2}$ units up means above $x-$axis and then we have the co-ordinates ${{p}_{2}}$ as ${{p}_{2}}\left( 1,\dfrac{1}{2} \right)$. Similarly we move from ${{p}_{2}}$ to ${{p}_{3}}$ away from $y-axis$ by $\dfrac{1}{4}$ units and we have the co-ordinates of ${{p}_{3}}$ as ${{p}_{3}}\left( 1+\dfrac{1}{4},\dfrac{1}{2} \right)={{p}_{3}}\left( \dfrac{5}{4},\dfrac{1}{2} \right)$. We move from ${{p}_{3}}$ to ${{p}_{4}}$ down by $\dfrac{1}{8}$ units. So we have to subtract the ordinate of ${{p}_{3}}$ by $\dfrac{1}{8}$ and have the co-ordinates ${{p}_{4}}\left( \dfrac{5}{4},\dfrac{1}{2}-\dfrac{1}{8} \right)={{p}_{4}}\left( \dfrac{5}{4},\dfrac{3}{8} \right)$. We move we move from ${{p}_{4}}$ to ${{p}_{5}}$ away from $y-axis$ by $\dfrac{1}{16}$ units and we have the co-ordinates ${{p}_{5}}\left( \dfrac{5}{4}+\dfrac{1}{16},\dfrac{3}{8} \right)={{p}_{5}}\left( \dfrac{21}{16},\dfrac{3}{8} \right)$. The co-ordinates of the points are ,
\[{{p}_{1}}\left( 1,0 \right),{{p}_{2}}\left( 1,\dfrac{1}{2} \right),{{p}_{3}}\left( 1+\dfrac{1}{4},\dfrac{1}{2} \right),{{p}_{4}}\left( 1+\dfrac{1}{4},\dfrac{1}{2}-\dfrac{1}{8} \right),{{p}_{5}}\left( 1+\dfrac{1}{4}+\dfrac{1}{16},\dfrac{1}{2}-\dfrac{1}{8} \right)...\]
We observe that as the point moves the $x-$coordinate of the point ${{p}_{n}}$ that s denoted as ${{x}_{n}}$ is the sum of $n$ terms of the sequence $1,\dfrac{1}{4},\dfrac{1}{16}...$. We see that it is an infinite GP with $a=1,r=\dfrac{1}{4}$ . If we take the limit $n\to \infty $ of the sum it will be equal to the sum of infinite GP series. So we have
\[\underset{n\to \infty }{\mathop{\lim }}\,{{x}_{n}}=1+\dfrac{1}{4}+\dfrac{1}{16}+...=\dfrac{1}{1-\dfrac{1}{4}}=\dfrac{4}{3}\]
We again observe the pints and see that moves the $y-$coordinate of the point ${{p}_{n}}$ that sis denoted as ${{y}_{n}}$ is the sum of first $n$ terms of the sequence $\dfrac{1}{2},\dfrac{-1}{8},\dfrac{1}{32}...$. It as infinite GP with $a=\dfrac{1}{2},r=\dfrac{-1}{4}$. If we take the limit $n\to \infty $ of the sum it will be equal to the sum of infinite GP series. So we have
\[\underset{n\to \infty }{\mathop{\lim }}\,{{y}_{n}}=\dfrac{1}{2}-\dfrac{1}{8}+\dfrac{1}{32}+...=\dfrac{1}{1-\left( -\dfrac{1}{4} \right)}=\dfrac{2}{5}\]
We have the required result as
\[\underset{n\to \infty }{\mathop{\lim }}\,{{p}_{n}}=\underset{n\to \infty }{\mathop{\lim }}\,\left( {{x}_{n}},{{y}_{n}} \right)=\left( \underset{n\to \infty }{\mathop{\lim }}\,{{x}_{n}},\underset{n\to \infty }{\mathop{\lim }}\,{{y}_{n}} \right)=\left( \dfrac{4}{3},\dfrac{2}{5} \right)\]
So the correct option is B. \[\]
Note:
We note that ${{x}_{1}}+{{x}_{2}}+{{x}_{3}}...=\underset{n\to \infty }{\mathop{\lim }}\,{{x}_{n}}=L$ then we say sequence ${{x}_{1}},{{x}_{2}},{{x}_{3}},...$ converges at $L$. The sequence is called a converging sequence. If the limit does not exist the sequence is called diverging sequence.