Question

A parallelogram is constructed on the vector, $\overrightarrow a = 3\overrightarrow p - \overrightarrow q $ and $\overrightarrow b = \overrightarrow p + 3\overrightarrow q $, given that $\left| {\overrightarrow p } \right| = \left| {\overrightarrow q } \right| = 2$ and the angle between$\vec p{\text{ and }}\vec q{\text{ is }}\dfrac{\pi }{3}$ . The length of a diagonal is
A.$4\sqrt 5 $
B.$4\sqrt 3 $
C.$4\sqrt 7 $
D.None of these

Answer 1

Hint- To solve this question, firstly we have to calculate the diagonal vectors $\overrightarrow a + \overrightarrow b $ and $\overrightarrow a - \overrightarrow b $, then for calculating the length of a diagonal, we have to find the magnitude of both the diagonal vectors by using the formula:
$
  \left| {\overrightarrow a + \overrightarrow b } \right| = \sqrt {{a^2} + {b^2} + 2ab\cos \theta } \\
  \left| {\overrightarrow a - \overrightarrow b } \right| = \sqrt {{a^2} + {b^2} - 2ab\cos \theta } \\
 $
Where, θ is the angle between the two vectors, i.e. a and b.


Complete step by step solution:
The diagonals of the parallelogram are represented by the vectors:
\[
  \overrightarrow a + \overrightarrow b = \left( {\overrightarrow {3p} - \overrightarrow q } \right) + \left( {\overrightarrow p + \overrightarrow {3q} } \right) = \overrightarrow {4p} + \overrightarrow {2q} \\
  {\text{and }}\overrightarrow a - \overrightarrow b = \left( {\overrightarrow {3p} - \overrightarrow q } \right) - \left( {\overrightarrow p + \overrightarrow {3q} } \right) = \overrightarrow {2p} - \overrightarrow {4q} \\
 \]

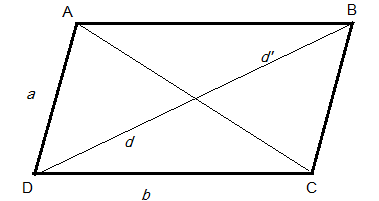
Now,
\[
  {\left| {\overrightarrow a + \overrightarrow b } \right|^2} = {\left| {\overrightarrow {4p} + \overrightarrow {2q} } \right|^2} = 16{\left| {\overrightarrow p } \right|^2} + 4{\left| {\overrightarrow q } \right|^2} + 16\overrightarrow {p.} \overrightarrow q \\
   = 16{\left( 2 \right)^2} + 4{\left( 2 \right)^2} + 16\left( 2 \right)\left( 2 \right)\cos \dfrac{\pi }{3} \\
   = 64 + 16 + 32{\text{ }}\left[ {\because \cos \dfrac{\pi }{3} = \dfrac{1}{2}} \right] \\
   = 112 \\
  \left| {\overrightarrow a + \overrightarrow b } \right| = \sqrt {112} = 4\sqrt 7 \\
 \]

Similarly, we can also find the other diagonal as:
$
  {\left| {\overrightarrow a - \overrightarrow b } \right|^2} = {\left| {\overrightarrow {2p} - \overrightarrow {4q} } \right|^2} = 4{\left| {\overrightarrow p } \right|^2} + 16{\left| {\overrightarrow q } \right|^2} - 16\overrightarrow p .\overrightarrow q \\
   = 4{\left( 2 \right)^2} + 16{\left( 2 \right)^2} - 16\left( 2 \right)\left( 2 \right)\cos \dfrac{\pi }{3} \\
   = 16 + 64 - 32 \\
   = 48 \\
  \left| {\overrightarrow a - \overrightarrow b } \right| = \sqrt {48} = 4\sqrt 3 \\
 $
Hence, the lengths of the diagonals are $4\sqrt 3 {\text{ and }}4\sqrt 7 .$
Option B and C are correct.

Additional Information: The addition of two vectors may also be understood by the law of parallelogram. It states that “if two vectors acting simultaneously at a point are represented in magnitude and direction by the two sides of a parallelogram drawn from a point, their resultant is given in magnitude and direction by the diagonal of the parallelogram passing through that point.” A parallelogram with vector sides $\overrightarrow a $ and $\overrightarrow b $ has diagonals as $\overrightarrow a + \overrightarrow b $ and $\overrightarrow a - \overrightarrow b $. The diagonal vectors will be addition and subtraction of these two vectors.



Note: In a parallelogram, opposite sides are equal and parallel, opposite angles are equal, and adjacent angles are supplementary. The diagonals of a parallelogram are not of equal length, and they bisect with each other. The longer diagonal is opposite to the larger of the parallelogram’s angles.