Question

A nickel is placed on a table. The number of nickels which can be placed around it, each tangent to it and to two others is:
A. 4
B. 5
C. 6
D. 8

Answer 1

Hint: In order to find the answer to the above question, we need to first draw a diagram. In the diagram draw a circle (which is the shape of a nickel). Then draw a few more nickels around this nickel. With the help of this we can calculate the angle of each triangle formed by joining the radius of all the circles.

Complete step by step solution:
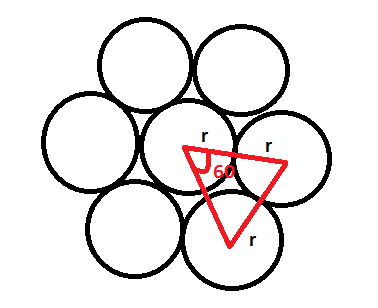
First draw a circle and draw two more circles around it.
Let the radius of each nickel be \[r\] .
Now join the centers of the nickels.
The triangle formed by joining the centers is an equilateral triangle who’s each side is equal to \[2r\] and each angle is of \[{60^ \circ }\] .
Similarly, if we draw more circles or nickels around the nickel, the radius of each nickel will be the same. On joining any of these radii we will get equilateral triangles with \[{60^ \circ }\] angle.
Therefore, every nickel that we add will make an angle of \[{60^ \circ }\] at the center.
But we know that the total angle at the center is \[{360^ \circ }\] , so to get the total number of nickels that can be placed around one nickel we use the formula
\[Total{\text{ }}number{\text{ }}of{\text{ }}circles = \dfrac{{{{360}^ \circ }}}{{{{60}^ \circ }}}\]
                                                \[ = 6\] .
Hence, we get that the total number of nickels that can be placed around one nickel is \[6\] .
So, the correct option is C. \[6\] .

Note: While solving such questions, always draw the diagram. With the help of the diagram solution can easily be drafted and it will finish in a very less amount of time. Also, remember that the total angle at the center of a circle is \[{360^ \circ }\] . In this question we have also kept in mind the properties of equilateral triangles.