Question

A motor car is travelling at $60m{{s}^{-1}}$ on a circular road of radius $1200m$. The speed is increasing in it at a rate of $4m{{s}^{-2}}$. The acceleration of the car will be given as,
$\begin{align}
  & A.3m{{s}^{-2}} \\
 & B.4m{{s}^{-2}} \\
 & C.5m{{s}^{-2}} \\
 & D.7m{{s}^{-2}} \\
\end{align}$

Answer 1

Hint: The radial acceleration is given as the ratio of the square of the velocity to the radius of the circular path taken. The value of tangential acceleration has been given. Take the resultant of both and reach the answers. These all may help you to solve this question.

Complete step-by-step solution:

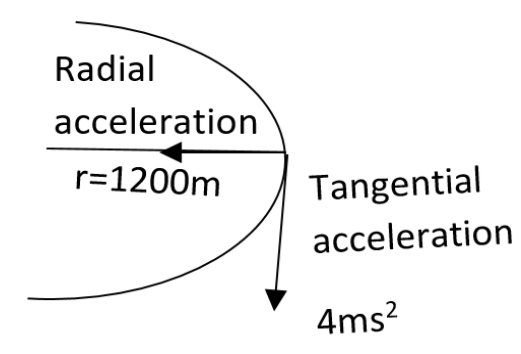
First of all, let us mention what all are given in the question. The tangential acceleration has been mentioned in the question as,
${{a}_{t}}=4m{{s}^{-2}}$
The velocity of the car traveling in the circular path is given as,
$V=60m{{s}^{-1}}$
And the radius of the circular path is given as,
$r=1200m$
As we all know, the radial acceleration or the centripetal acceleration is given as the equation,
${{a}_{r}}=\dfrac{{{v}^{2}}}{r}$
Substituting the values in it will give,
${{a}_{r}}=\dfrac{60\times 60}{1200}=3m{{s}^{-2}}$
Therefore the net acceleration of the car is given by taking the results of the tangential and radial acceleration. This can be written as,
$a=\sqrt{{{a}_{t}}^{2}+{{a}_{r}}^{2}}$
Let us substitute the values of accelerations in it,
$a=\sqrt{{{4}^{2}}+{{3}^{2}}}=\sqrt{25}=5m{{s}^{-2}}$
Therefore the resultant acceleration is obtained. Therefore the correct answer is obtained as option C.

Note: Radial acceleration is also called centripetal acceleration as it is directed towards the center. If the speed of an object is not fixed, then the tangential acceleration will also be there. The tangential acceleration is in a direction tangential to the path of the object. The radial direction is the direction, which begins at the center of a circle and goes directly outwards. As the centripetal acceleration points inwards, we provide it a negative sign.