Question

A motor boat going downstream in a flowing river overcame a raft at a point P. One hour later it turned back and after some time passed the raft at a distance \[6Km\] from the point P. After reverting how much time was taken by the boat to meet the raft again? (i.e., second time)
\[\begin{align}
  & A)2hr \\
 & B)1hr \\
 & C)30\min \\
 & D)3hr \\
\end{align}\]

Answer 1

Hint: Since the boat is travelling in the direction of river flow, the velocity of boat will be affected by the river velocity. While returning, velocity of boat will be the difference in boat velocity and water velocity. By making equations using the equation for velocity, substituting the values accordingly and equating them we can find the time taken by boat to meet the raft after reverting.

Formula used:
\[\text{v = }\dfrac{\text{distance}\left( d \right)}{\text{time}\left( t \right)}\]

Complete answer:

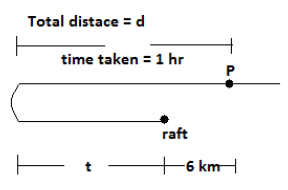
Let \[x\] be the velocity of boat, \[y\] be the velocity of water, \[d\] be the distance travelled by the boat in \[\text{60minutes }\left( \text{1hr} \right)\]
We have,
Velocity, \[\text{v = }\dfrac{\text{distance}\left( d \right)}{\text{time}\left( t \right)}\]
Then,
\[d=\left( x+y \right)1\] ----------- (1)
Assume that, boat meets the raft in time \[t\], and the raft is \[6km\] away from the point P. Then the distance covered by the boat during the upward journey in time \[t\] is,
\[\left( x-y \right)t=d-6=\] ----------- (2)
During the total time\[1+t\] raft travels \[6km\] distance. Then,
\[6=y\left( 1+t \right)\] --------------- (3)
Substitute equation 3 and 1 in equation 2. We get,
\[\left( x-y \right)t=\left( x+y \right)1-y\left( 1+t \right)\]
\[xt-yt=x+y-y-yt\]
Then,
\[xt=x\]
\[t=1hr\]
Time taken by the boat to meet the raft is \[1hr\].

Therefore, the correct option is option (B).

Note:
If a boat is travelling along the direction of a river flow, the net velocity of the boat will be the sum of its individual velocity and river velocity. And if it is travelling against the river flow, the net velocity of the boat will be different in the boat velocity and river velocity.