Question

A monkey is ascending a branch with constant acceleration. If the breaking strength is 160% of the monkey’s weight, what is the maximum acceleration permitted for the monkey?

Answer 1

Hint: As, the monkey is ascending the branch, the tension in the branch increases. As the acceleration of the monkey increases, it will cause an increase in tension of the branch. The maximum tension the branch can take is the breaking strength of the branch. We can find the acceleration by finding the net force acting on the monkey.

Formula used:
${a_{\max }} = \dfrac{{{T_{\max }} - mg}}{m}$

Complete answer:
Let’s draw a free body diagram, from the given questions, so that we can understand the forces involved.

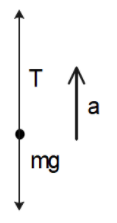
Here, T represents the tension of the branch, m is the mass of the monkey and a is the acceleration of the monkey.
Here, in this case the force is given by,
$\eqalign{
  & {F_{net}} = ma \cr
  & \Rightarrow T - mg = ma \cr
  & \Rightarrow a = \dfrac{{T - mg}}{m} \cr} $
Here, you need to understand that the acceleration of the monkey will appear in the upward direction, while the monkey is ascending the branch, i.e. when the tension of the branch is more than the weight of the monkey.
The breaking stress of the branch is the maximum tension the string can handle, without breaking. It is mentioned in the question that the breaking stress of the branch is 160% of the monkey’s weight. So, when maximum tension is applied, the monkey will have the maximum acceleration. Thus, we have
${T_{\max }} = \dfrac{{160}}{{100}}mg = 1.6mg$
So, the maximum acceleration the monkey can have is,
$\eqalign{
  & {a_{\max }} = \dfrac{{{T_{\max }} - mg}}{m} \cr
  & \Rightarrow {a_{\max }} = \dfrac{{1.6mg - mg}}{m} = \dfrac{{0.6mg}}{m} \cr
  & \Rightarrow {a_{\max }} = 0.6g \cr} $
Here, g is the acceleration due to gravity.
Therefore, the maximum acceleration permitted for the monkey is 1.6g.

Note:
Always draw a free body diagram, to analyze the forces acting on the system. It helps in knowing the cancellation or interaction of forces and the direction of acceleration of the body. In a free body diagram (or F.B.D.) consider the object of interest as a point object and draw the forces acting on it.
The above problem is based on Newton’s second law – the object will accelerate only if the force acting is unbalanced i.e., the net force on the object must not be zero.