Question

A metallic solid of volume 1,500 $c{{m}^{3}}$ melted and drawn into the form of a wire of height 14 cm. Find the radius of the wire. (Use $\pi =\dfrac{22}{7}$)
(a) $2\sqrt{5}cm$
(b) $4\sqrt{5}cm$
(c) $5.83cm$
(d) $3\sqrt{5}cm$

Answer 1

Hint: Whenever a metallic solid is converted from one shape to another, the volume of the metal used remains the same. This is also known as conservation of volume. Also, there are some formulas that will be used to solve this question. The volume of the cylinder is given by the formula $\pi {{r}^{2}}h$.
Complete step-by-step answer:
Before proceeding the question, we must know all the concepts and the formula that will be required to solve this question.
By the conservation of volume, if a metallic solid is converted from one shape to another, the volume of the metal in both the shapes remains the same.
The volume of a cylinder having radius r and height h is given by the formula,
$V=\pi {{r}^{2}}h...........\left( 1 \right)$
In the question, it is given that a metallic solid of volume 1,500 $c{{m}^{3}}$ melted and drawn into the form of a wire of height 14 cm. and required to find the radius of the cylindrical wire that is formed.
Let us assume a variable r which represents the radius of the cylindrical wire formed.
From formula $\left( 1 \right)$, the volume of cylinder having radius r and height h = 14cm is,

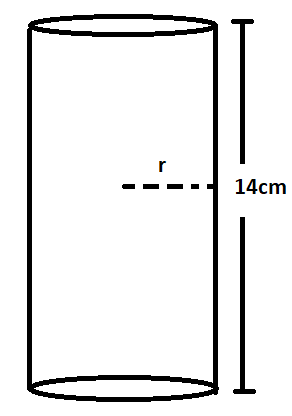
$V=\pi {{r}^{2}}\left( 14 \right)$
Substituting $\pi =\dfrac{22}{7}$ in the above equation, we get,
$\begin{align}
  & V=\dfrac{22}{7}{{r}^{2}}\left( 14 \right) \\
 & \Rightarrow V=44{{r}^{2}} \\
\end{align}$
From the concept of conservation of volume, we can say that this volume is equal to the volume of the solid from which the cylinder is formed. In the question, the volume of the sphere is given as 1,500 $c{{m}^{3}}$. Equating the above obtained volume to 1500, we get,
$\begin{align}
  & 44{{r}^{2}}=1500 \\
 & \Rightarrow {{r}^{2}}=\dfrac{1500}{44} \\
 & \Rightarrow {{r}^{2}}=\dfrac{750}{22} \\
 & \Rightarrow {{r}^{2}}=34.09 \\
 & \Rightarrow r=5.83cm \\
\end{align}$
The answer is option (c).
Note: There is a possibility that one may commit a mistake while applying the formula of the cylinder. It is a very common mistake that students forget to write units of radius and this mistake may lead us to an incorrect answer.