Question

A metallic right circular cone 20cm high and whose vertical angle is ${90^ \circ }$ is cut into two parts at the middle point of its axis by a plane parallel to the base. If the frustum so obtained be drawn into a wire of diameter $\dfrac{1}{{16}}cm$ , find the length of the wire.

Answer 1

Hint: In this question remember that volume of frustum will be equal to volume of volume of wire of cylindrical shape and also remember that Volume of frustum is equal to \[\dfrac{1}{3}\pi \left( {{R^2}H - {r^2}h} \right)\] here R and r be the radius of circular ends of the frustum and H is the height of cone and h is the height of frustum.

Complete step-by-step answer:
According to the given question we have to find the length of the wire made from Frustum so first we will find the volume of frustum
Let OCD take as the solid metallic right circular cone with height 20 cm. now suppose this cone is cut by a plane parallel to its base of point Q such that OQ = PQ

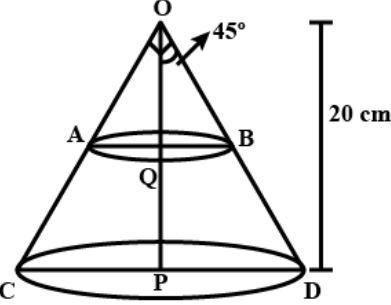
Let R and r be the radius of circular ends of the frustum CDBA
OP = 20cm, PD = R, OQ = 10cm, QB = r
Now in right-triangle OPD we know that $\angle POD = {45^ \circ }$
Snice we know that $\tan \theta = \dfrac{{base}}{{perpendicular}}$
Therefore, $\tan {45^ \circ } = \dfrac{{PD}}{{OP}} = \dfrac{R}{{20}}$ $\left( {\because \tan {{45}^ \circ } = 1} \right)$
So, R = 20cm
Now in triangle OQB we know that $\angle QOB = {45^ \circ }$
Therefore, $\tan {45^ \circ } = \dfrac{{QB}}{{OQ}} = \dfrac{r}{{10}},r = 10cm$
So, r = 10 cm
According to the question Volume of frustum = volume of wire (cylindrical shape)
Since, Volume of frustum = \[\dfrac{1}{3}\pi \left( {{R^2}H - {r^2}h} \right)\]And volume of cylinder = \[\pi {\left( {r'} \right)^2}l\] and r’ of wire = $\dfrac{1}{{32}}cm$
\[\dfrac{1}{3}\pi \left( {{R^2}H - {r^2}h} \right) = \pi {\left( {r'} \right)^2}l\]
Substituting the values in the above equation we get
\[\dfrac{1}{3}\left( {{{\left( {20} \right)}^2} \times 20 - {{\left( {10} \right)}^2} \times 10} \right) = {\left( {\dfrac{1}{{32}}} \right)^2}l\]
\[\dfrac{1}{3}\left( {400 \times 20 - 100 \times 10} \right) = \dfrac{1}{{1024}}l\]
\[l = \dfrac{{7000 \times 32 \times 32}}{3} = 2389333.33cm\]
Therefore, the length of the wire will be 2389333.33 cm

Note: The trick behind the above question was the concept equilibrium let discuss how this concept was responsible for the outcome of the solution. So, as first we used the concept of equilibrium as we knew that wire is made of solid frustum so, remember that whenever we change the shape without losing any material then the volume of initial shape is equal to the volume of final shape of material but when we change the shape the dimensions change. So, using this concept it made easy for us to find the length of wire.