Question

A metallic right circular cone 20cm high and whose vertical angle is 60 degrees is cut into two parts at the middle of its height by a plane parallel to its base. If the frustum so obtained be drawn into a wire of diameter $\dfrac{1}{{16}}$​cm, find the length of wire.

Answer 1

Hint: In order to solve this problem we need to draw the rough figure and solve to find the volume of frustum before that we need to find the radius of frustum and then we will equate the volume of frustum with the volume of wire considering the wire as cylinder so that we can find the length of the wire.

Complete step-by-step answer:

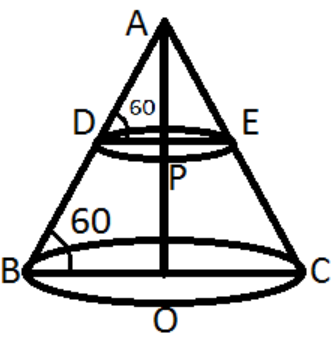
Above figure is the figure of the cone ABC and the frustum DEBC.
Let DP = ${r_1}$, BO = ${r_2}$, AO = 20cm (given) and angle ABO = angle ADE = 60 degrees.
And we know that the plane cuts the cone at half of its height so AP = 10cm.
Now we find ${r_1}$, so we do
$
  \tan 60 = \dfrac{{AP}}{{{r_1}}} = \dfrac{{10}}{{{r_1}}} \\
  \sqrt 3 = \dfrac{{10}}{{{r_1}}} \\
  {r_1} = \dfrac{{10}}{{\sqrt 3 }} \\
$
Now we will find ${r_2}$,
So, we do:
$
  \tan 60 = \dfrac{{20}}{{{r_2}}} \\
  {r_2} = \dfrac{{20}}{{\sqrt 3 }} \\
$
Therefore the volume of the frustum DECB we get,
Volume DECB = $(\pi \times \dfrac{{OP}}{3})(r_1^2 + r_2^2 + {r_1}{r_2})$
On putting the respect values we get,
Volume DECB,
$
   \Rightarrow \left( {\pi \times \dfrac{{10}}{3}} \right)\left( {{{\left( {\dfrac{{10}}{{\sqrt 3 }}} \right)}^2} + {{\left( {\dfrac{{20}}{{\sqrt 3 }}} \right)}^2} + \left( {\dfrac{{20}}{{\sqrt 3 }}} \right)\left( {\dfrac{{10}}{{\sqrt 3 }}} \right)} \right) \\
   \Rightarrow \dfrac{{7000\pi }}{9} \\
$
As, it is given in question that we have to convert the volume of frustum into wire of diameter $\dfrac{1}{{16}}$ cm.
So, we equate the volume of frustum DECB with the volume of wire.
Let the length of the wire be $l$ and its radius is $R = \dfrac{D}{2} = \dfrac{1}{{16 \times 2}} = \dfrac{1}{{32}}$.
The volume of the wire is $\pi {R^2}l$.
Equating the volume of wire with the volume of the frustum we get,
$
   \Rightarrow \dfrac{{7000\pi }}{9} = \pi {R^2}l \\
   \Rightarrow \dfrac{{7000\pi }}{9} = \pi {\left( {\dfrac{1}{{32}}} \right)^2}l \\
$
On solving we got the value of $l$ as,
$
   \Rightarrow l = \dfrac{{7000 \times 32 \times 32}}{9} \\
   \Rightarrow l = 796444.444cm \\
$
So, the length in cm is $796444.444$cm.
In meters the length is $l$ = $7964.44$m.
Therefore the answer to this problem is 7964.44m.

Note In such types of problems drawing diagrams will make your questions almost solved if you know the basics formulae. With the help of given angle in a right angled triangle we have found the radius of frustum and we also have found the volume of frustum by using the formula $(\pi \times \dfrac{h}{3})(r_1^2 + r_2^2 + {r_1}{r_2})$ where h is the height and r is the radius. We have equated the volume of frustum with the volume of wire to get the length of the wire since the wire needs to be recasted from the frustum.