Question

A metal pipe is 98cm long. The inner diameter of the cross-section is 6cm and outer diameter is 6.6cm. Find
(1) Its inner surface area
(2) Outer surface area
(3) Total surface area.

Answer 1

Hint:In this problem, we have to find the inner surface area, outer surface area and the total surface area of a metal pipe whose length is 98cm, the inner diameter is 6cm and the outer diameter is 6.6cm. We can find the inner radius and the outer radius and substitute in its suitable formula to get the inner surface area and the outer surface area. We can then substitute the required data in the total surface area formula to get the answer.

Complete step-by-step solution:
Here we have to find the inner surface area, outer surface area and the total surface area of a metal pipe whose length is 98cm, the inner diameter is 6cm and the outer diameter is 6.6cm.
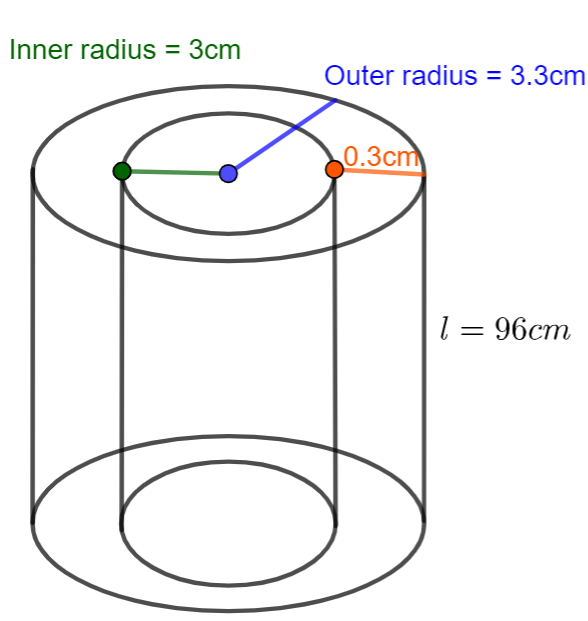
We know that diameter is twice the radius, so we can find the radius.
Here we can see that the pipe is in cylindrical shape.
Let the radius of inner surface be r, then
\[\Rightarrow r=\dfrac{6}{2}=3cm\]
Let the radius of outer surface be R, the
\[\Rightarrow R=\dfrac{6.6}{2}=3.3cm\]

We know that the formula to find the outer surface area is
Outer surface area of pipe = \[2\pi Rl\]
We can now substitute the value of R and Length in the above formula, we get
\[\begin{align}
  & \Rightarrow 2\times \dfrac{22}{7}\times 3.3\times 98 \\
 & \Rightarrow 44\times 3.3\times 14=2032.8c{{m}^{2}} \\
\end{align}\]
The outer surface area is 2032.8sq.cm. …… (1)
We know that the formula to find the inner surface area is
Inner surface area of pipe = \[2\pi rl\]
We can now substitute the value of r and Length in the above formula, we get
\[\begin{align}
  & \Rightarrow 2\times \dfrac{22}{7}\times 3\times 98 \\
 & \Rightarrow 44\times 3\times 14=1848c{{m}^{2}} \\
\end{align}\]
The inner surface area = 1848sq.cm. ……… (2)
We can now find the total surface area whose formula is
Total surface area of a pipe = \[Inner+Outer+2\left[ \pi \left( {{R}^{2}}-{{r}^{2}} \right) \right]\]
We can now substitute the value of outer radius inner radius and the surface areas in the above formula, we get
\[\begin{align}
  & \Rightarrow 1848+2032.8+2\left[ \dfrac{22}{7}\left( {{\left( 3.3 \right)}^{2}}-{{\left( 3 \right)}^{2}} \right) \right] \\
 & \Rightarrow 3880.8+11.88=3892.68 \\
\end{align}\]
The total surface area is 3892.68sq.cm.
Therefore, the outer surface area is 2032.8sq.cm, the inner surface area = 1848sq.cm and the total surface area is 3892.68sq.cm.

Note: We should always remember some of the mensuration formulas such as Outer surface area of pipe is \[2\pi Rl\], Inner surface area of pipe is \[2\pi rl\] and the Total surface area of a pipe = \[Inner+Outer+2\left[ \pi \left( {{R}^{2}}-{{r}^{2}} \right) \right]\] . Here we have two radii which are differentiated in the assumed variable.