Question

A mass of point 0.5kg is suspended from a wire, if the length of the wire is increased by $3\,mm$what is the work done?
A. $4.5 \times {10^{ - 3}}\,J$
B. $7.5 \times {10^{ - 3}}\,J$
C. $9.3 \times {10^{ - 3}}\,J$
D. $2.5 \times {10^{ - 3}}\,J$

Answer 1

Hint: By using the equation for Young's modulus which is the ratio of stress to strain we can arrive at an equation for force.
Work done is a product of force and displacement. Hence, we can write
$dw = Fdx$
By integrating this equation, we can reach the equation to find work done in elongating the wire.

Complete step by step answer:
Let the length of the wire be $L$ and the cross-sectional area by $A$
We know that Young's modulus is given by the equation
$Y = \dfrac{{stress}}{{strain}}$ …………...(1)
Here, Stress is the force per unit area.
$stress = \dfrac{F}{A}$
Strain is the ratio of change in length by original length
$strain = \dfrac{x}{L}$
Let us substitute these values in equation (1). Then, we get
$Y = \dfrac{{\dfrac{F}{A}}}{{\dfrac{x}{L}}}$
$ \Rightarrow F = \dfrac{{YAx}}{L}$ ……………….(2)

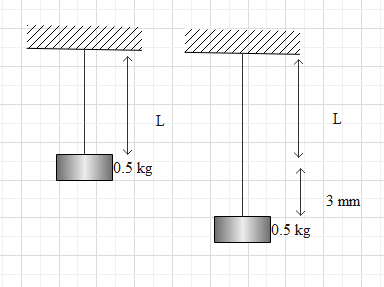
The elongation of the wire is given as
 $l = 3\,mm = 3 \times {10^{ - 3}}\,m$
Work done is a product of force and displacement. Hence, we can write
$dw = Fdx$
Now let us substitute the value of force that we obtained.
$ \Rightarrow dw = \dfrac{{YAx}}{L}dx$ (3)
Now let us integrate this
$\int {dw} = \dfrac{{YA}}{L}\int\limits_0^l x dx$
$ \Rightarrow w = \dfrac{{YA}}{L}\left[ {\dfrac{{{x^2}}}{2}} \right]_0^l$
$ \Rightarrow w = \dfrac{{YAl}}{L}\dfrac{l}{2}$
In equation (2). If we substitute $x = l$ we get
$F = \dfrac{{YAl}}{L}$
Thus, work can be written as
$w = \dfrac{{mgl}}{2}$
On substituting the given values we get,
$w = \dfrac{{0.5\,kg \times 10 \times 3 \times {{10}^{ - 3}}}}{2}$
$\therefore w = 7.5 \times {10^{ - 3}}\,J$

Therefore, the correct answer is option B.

Note:
Force is mass times acceleration. In the question, mass is given. Force causing elongation is the weight which is given by the equation
$w = mg$. Since the mass of the body is given, we should multiply it with acceleration due to gravity to get weight.
Here, we used Young’s modulus since the force produced a change in length. Young’s modulus is the ratio of longitudinal stress to longitudinal strain. In the case where the volume change is involved, we should use bulk modulus. Bulk modulus is the ratio of volumetric stress to volumetric strain.