Question

A mass of M kg is suspended by a weightless string. The horizontal force that is required to displace it until the string makes an angle of 45 degrees with the initial vertical direction is
$
  {\text{A}}{\text{.Mg(}}\sqrt {\text{2}} {\text{ + 1)}} \\
  {\text{B}}{\text{.Mg}}\sqrt {\text{2}} \\
  {\text{C}}{\text{.}}\dfrac{{{\text{Mg}}}}{{\sqrt {\text{2}} }} \\
  {\text{D}}{\text{.Mg(}}\sqrt {\text{2}} {\text{ - 1)}} \\
$

Answer 1

Hint: Drawing a rough figure and analyzing from that will solve your half of the problem. Using work energy theorem will solve the rest of your problem.
Formula Used – Sum of all the work = Change in kinetic energy.

Complete Step-by-Step solution:

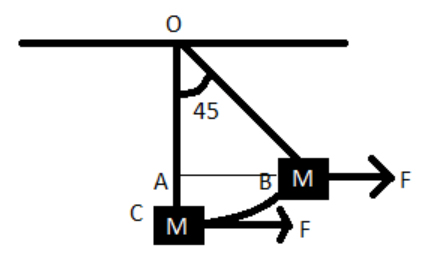
We will use the work energy theorem on analyzing the figure above.
Work energy theorem is,
Total work = Change in kinetic energy = $\Delta {\text{K}}$
Here on the block at C three types of work done are taking place those are,
Work done by the wire OC, work done by gravity (Mg), work done by force F.
So, according to work energy theorem,
${{\text{W}}_{{\text{Gravity}}}}{\text{ + }}{{\text{W}}_{\text{F}}}{\text{ + }}{{\text{W}}_{{\text{Tension}}}}{\text{ = }}$ Change in kinetic energy …………..(1)
Now we can say that work done by tension is zero when the block moves from C to B since the same forces are applied at C and B both and displacement due to the tension is zero so work done is also zero.
Therefore ${{\text{W}}_{{\text{Tension}}}}$ = 0.
Also we can say that change in kinetic energy is zero since the velocity at C and B is zero because the block is at rest whatever may be the velocity in between we only need to consider the initial and final velocity.
So, we can do ${\text{}{\delta K}}$=0.
And work done by gravity is something because the block has movement in or opposite to the direction of gravity.
So, work done by gravity on the block is ${{\text{W}}_{{\text{Gravity}}}}$= Mg(AC).
Let AC = h.
So, ${{\text{W}}_{{\text{Gravity}}}}$= -Mgh.
Since, work done is force multiplied by the displacement of the body in the direction of force. We have taken here work done negatively because the displacement Is opposite to the direction of force.
Now work done by force F is ${{\text{W}}_{\text{F}}}$ = F(AB)
So, on putting these values in equation (1) we get,
0 - Mgh + F(AB) = 0
So, ${\text{F = }}\dfrac{{{\text{Mgh}}}}{{{\text{AB}}}}$ ……(2)
Now we will calculate $\dfrac{{\text{h}}}{{{\text{AB}}}}{\text{ = }}\dfrac{{{\text{AC}}}}{{{\text{AB}}}}$
Let us take the length of the wire be L.
So, OC = OB = L
And the angle COB is 45 degrees.
So, we get AB = $\text{L}\sin45$ = $\dfrac{{\text{L}}}{{\sqrt {\text{2}} }}$
And AC = OC – OA = ${\text{L - }}\dfrac{{\text{L}}}{{\sqrt {\text{2}} }}$

So, $\dfrac{{\text{h}}}{{{\text{AB}}}}{\text{ = }}\dfrac{{{\text{AC}}}}{{{\text{AB}}}}{\text{ = }}\left( {\dfrac{{{\text{L}}\left( {{\text{1 - }}\dfrac{{\text{1}}}{{\sqrt {\text{2}} }}} \right)}}{{\dfrac{{\text{L}}}{{\sqrt {\text{2}} }}}}} \right) = \sqrt 2 - 1$ …………(3)
From equation (2) and (3) we can say $F = Mg(\sqrt 2 - 1)$.
Hence, the correct option is D.

Note – To get the right answer to this problem we need to know that the work-energy theorem states that the net work done by the forces on an object equals the change in its kinetic energy and the we have just solved and get the values of work done on analysing the figure then solved the equation to get the value of force. In these problems drawing diagrams is a must. Solving problems without diagrams is next to impossible.