Question

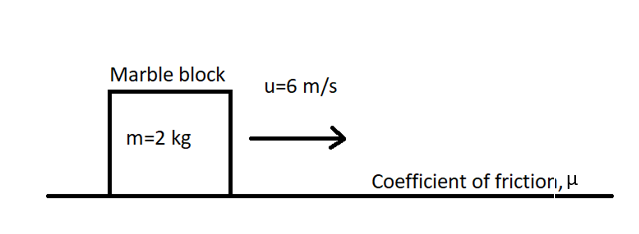
A marble block of mass $2\;kg$ lying on ice when given a velocity of $6\;m{s^{ - 1}}$ is stopped by friction in $10\;s$. Then the coefficient of friction is ( Take $g = 10\;m{s^{ - 2}}$)

A. $0.06$
B. $0.03$
C. $0.04$
D. $0.01$

Answer 1

Hint: From the question, the marble block of a defined mass moves with an initial velocity on the surface having some friction with desired coefficient of friction and also the stopping time of the marble block is given. By using the Newton’s law of motion equation, the deceleration of the body can be obtained. And then using that deceleration of the body in the relation between the deceleration of body and coefficient of friction, the coefficient of friction of the surface can be calculated.

Useful formula:
Newton’s law of motion is given by,
$v = u + at$
Where, $v$ is the final velocity of the body, $u$ is the initial velocity of the body, $a$ is the acceleration of the body and $t$ is the time taken by the body.

Deceleration of the body due to friction is given by,
$a = \mu g$
Where, $a$ is the deceleration of the body, $\mu $ is the coefficient of friction and $g$ is the acceleration due to gravity.

Complete step by step answer:
Given,
The mass of the marble block, $m = 2\;kg$
The initial velocity of the marble block, $u = 6\;m{s^{ - 1}}$
The time taken to stop the marble block, $t = 10\;s$
The acceleration due to gravity, $g = 10\;m{s^{ - 2}}$
Since, the marble block tends to rest finally, then the final velocity of the marble block, $v = 0\;m{s^{ - 1}}$

Newton’s law of motion is given by,
$v = u + at\;.........................................\left( 1 \right)$
By substituting the values of initial velocity, final velocity and time taken by the block in the equation (1),
$
  0\;m{s^{ - 1}} = 6\;m{s^{ - 1}} + a\left( {10\;s} \right) \\
  0 = 6 + 10a \\
  10a = - 6 \\
  a = - \dfrac{6}{{10}}\;m{s^{ - 2}} \\
  a = - 0.6\;m{s^{ - 2}} \\
 $
The negative sign indicates the deceleration of the marble block.

Deceleration of the body due to friction is given by,
$a = \mu g\;..........................................\left( 2 \right)$
By substituting the values of deceleration and acceleration due to gravity in equation (2), we get
$ 0.6\;m{s^{ - 2}} = \mu \times 10\;m{s^{ - 2}} \\
  \mu = \dfrac{{0.6}}{{10}} \\
  \mu = 0.06 \\ $

Hence, the option (A) is correct.

Note:
The marble block tends to rest after some time, then the final velocity must be zero. Since, the body tends to decelerate then the deceleration value is always in the negative sign and for finding the coefficient of friction value, the deceleration must be taken in positive.