
A manufacturer considers that men and women workers are equally efficient and so he pays them at the same rate. He has 30 workers (male and female) and 17 units capital; which he uses to produce two types of goods A and B. To produce one unit of A,2 workers and 3 units of capital are required while 3 workers and 1 unit of capital is required to produce one unit of B. if A and B are priced at $Rs.100$ and $Rs.120$ per unit respectively. How should he use his resources to maximize the total revenue? Form the LPP and solve graphically.
Do you agree with this view of the manufacturer that men and women workers are equally efficient and so should be paid at the same rate?
A). 1260
B). 1130
C). 1290
D). 3421
Answer
571.5k+ views
Hint: Here in the given question we need to make the equations according to the given condition we have to find the equation of Z then we have to draw the graph and according to the graph we have to find the value of Z and find out where the Z is maximum or minimum we will put the value of corner points in the Z equation before starting the problem you have to read the question 2 to 3 times because the given data is not given in these type of questions we have to make the data by our own.
Complete step-by-step solution:
So according to the question,
Let x and y be the number of goods of type A and of type B respectively
Therefore, the number of labors $=2x+3y$
As 30 units of labour are available
$\therefore 2x+3y\le 30$
Similarly, Constraint for capital is
$3x+y\le 17$
And non-zero constraints are
$x\ge 0$, $y\ge 0$
Objective function is
$Z=100x+120y$
Consider
$2x+3y=30$
For the point A here, we will put the value of x=0 in the above equation we will get,
$\begin{align}
& 2\left( 0 \right)+3y=30 \\
&\Rightarrow +3y=30 \\
&\Rightarrow y=\dfrac{30}{3} \\
&\Rightarrow y=10 \\
\end{align}$
Here we will get point \[A\text{ }\left( 0,\text{ }10 \right)\]
Let’s go for the point B we will put x =3,
$\begin{align}
& 2\left( 3 \right)+3y=30 \\
&\Rightarrow 6+3y=30 \\
&\Rightarrow 3y=30-6 \\
&\Rightarrow 3y=24 \\
&\Rightarrow y=\dfrac{24}{3} \\
&\Rightarrow y=8 \\
\end{align}$
So here we will get the point \[B\text{ }\left( 3,8 \right)\]
$2x+3y=30$ passes through \[A\text{ }\left( 0,\text{ }10 \right)\text{ }and\text{ }B\text{ }\left( 3,8 \right)\]
Consider,
$3x+y=17$
Where $x=3$, then $y=8$
$\begin{align}
& 3\left( 3 \right)+y=17 \\
&\Rightarrow 9+y=17 \\
&\Rightarrow y=17-9 \\
&\Rightarrow y=8 \\
\end{align}$
Where $y=0$, then $x=\dfrac{17}{3}$
$\begin{align}
& 3x+\left( 0 \right)=17 \\
&\Rightarrow 3x=17 \\
&\Rightarrow x=\dfrac{17}{3} \\
\end{align}$
$3x+y=17$ passes through $C\left( 3,8 \right)\,\,and\,\,B\left( \dfrac{17}{3},0 \right)$
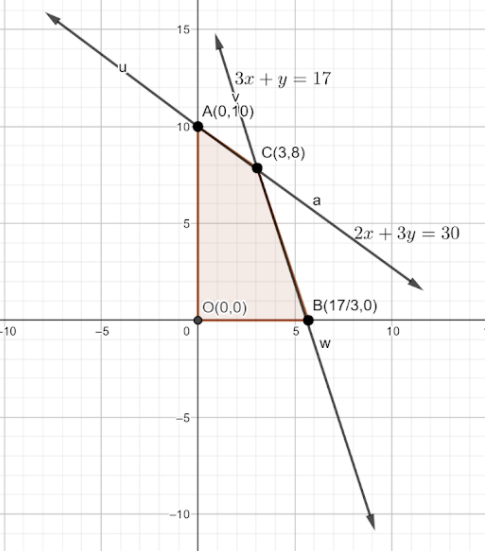
Further above two equations intersect at $C\left( 3,8 \right)$, vertices of the feasible region are $A\left( 0,10 \right),O\left( 0,0 \right),B\left( \dfrac{17}{3},0 \right)\,\,and\,\,C\left( 3,8 \right).$
At, $A\left( 0,10 \right),Z=100(0)+120\left( 10 \right)=Rs.1200 $
$O(0,0), Z=100\left( 0 \right)+120\left( 0 \right)=Rs.0 $
$B\left( \dfrac{17}{3},0 \right),Z=100\left( \dfrac{17}{3} \right)+120\left( 0 \right)=Rs.566.67 $
$C\left( 3,8 \right),Z=100\left( 3 \right)+120\left( 8 \right)=Rs.1260 $
Thus, the maximum value of $Z=Rs.1260$ at x=3 and y=8.
Yes, the view of manufacturers that men and women workers are equally efficient is correct and so they should be paid at the same rate.
Hence, the answer is $Rs.1260$
Note: Alternate solution:
Let x units of A and y units of B be produced by the manufacturer. The price of one unit of A is Rs.100 and the price of one unit of B is Rs.120. Therefore, the total price of x units of A and y units of B or the total revenue is Rs. (100x + 120y).
$Z=100x+120y....\left( i \right)$
One unit of A requires 2 workers and one unit of B requires 3 workers. Therefore, x units of A and y units of B require (2x + 3y) workers. But the manufacturer has 30 workers. 2x + 3y s 30 workers
$2x+3y\le 30...\left( ii \right)$
Similarly, one unit of A requires 3 units of capital and one unit of B requires 1 unit of capital. Therefore, x units of A and y units of B require (3x + y) units of capital. But the manufacturer has 17 units of capital.
$3x+y\le 17...\left( iii \right)$
Thus, the given linear programming problem is
Maximize Z = 100x + 120y
subject to the constraints
\[\begin{align}
& \begin{array}{*{35}{l}}
2x\text{ }+\text{ }3y\text{ }\le \text{ }30 \\
3x\text{ }+\text{ }y\,\,\le \text{ }17 \\
\end{array} \\
&\Rightarrow x\ge 0...\left( iv \right) \\
&\Rightarrow y\ge 0...\left( v \right) \\
\end{align}\]
Now we will plot the graph on a plot of above constants or inequalities (ii),(iii),(iv), and (v). we get shaded regions as feasible regions having corner points A, O, B and C. The feasible region determined by the given constraints can be diagrammatically represented as
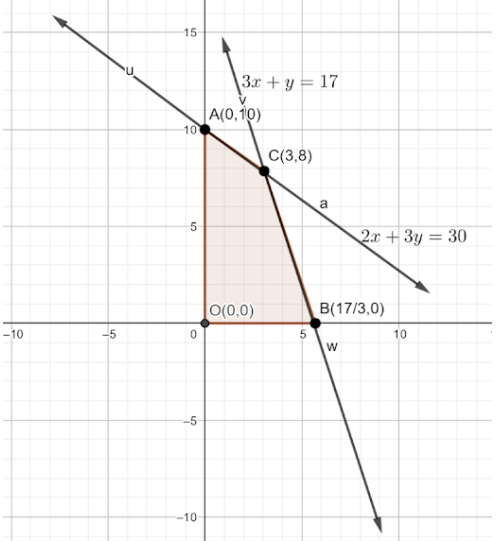
For the coordinates of C,
Two equations (ii) and (iii) are solved and we get coordinate of C = (3, 8)
Now, the value of Z is evaluated at the corner point as:
Therefore, maximum revenue is $Rs.1260$ when 2 workers and 8 units capital are used for production. Yes, although women workers have less physical efficiency but it can be managed by her other efficiency
Complete step-by-step solution:
So according to the question,
Let x and y be the number of goods of type A and of type B respectively
Therefore, the number of labors $=2x+3y$
As 30 units of labour are available
$\therefore 2x+3y\le 30$
Similarly, Constraint for capital is
$3x+y\le 17$
And non-zero constraints are
$x\ge 0$, $y\ge 0$
Objective function is
$Z=100x+120y$
Consider
$2x+3y=30$
For the point A here, we will put the value of x=0 in the above equation we will get,
$\begin{align}
& 2\left( 0 \right)+3y=30 \\
&\Rightarrow +3y=30 \\
&\Rightarrow y=\dfrac{30}{3} \\
&\Rightarrow y=10 \\
\end{align}$
Here we will get point \[A\text{ }\left( 0,\text{ }10 \right)\]
Let’s go for the point B we will put x =3,
$\begin{align}
& 2\left( 3 \right)+3y=30 \\
&\Rightarrow 6+3y=30 \\
&\Rightarrow 3y=30-6 \\
&\Rightarrow 3y=24 \\
&\Rightarrow y=\dfrac{24}{3} \\
&\Rightarrow y=8 \\
\end{align}$
So here we will get the point \[B\text{ }\left( 3,8 \right)\]
$2x+3y=30$ passes through \[A\text{ }\left( 0,\text{ }10 \right)\text{ }and\text{ }B\text{ }\left( 3,8 \right)\]
Consider,
$3x+y=17$
Where $x=3$, then $y=8$
$\begin{align}
& 3\left( 3 \right)+y=17 \\
&\Rightarrow 9+y=17 \\
&\Rightarrow y=17-9 \\
&\Rightarrow y=8 \\
\end{align}$
Where $y=0$, then $x=\dfrac{17}{3}$
$\begin{align}
& 3x+\left( 0 \right)=17 \\
&\Rightarrow 3x=17 \\
&\Rightarrow x=\dfrac{17}{3} \\
\end{align}$
$3x+y=17$ passes through $C\left( 3,8 \right)\,\,and\,\,B\left( \dfrac{17}{3},0 \right)$
Further above two equations intersect at $C\left( 3,8 \right)$, vertices of the feasible region are $A\left( 0,10 \right),O\left( 0,0 \right),B\left( \dfrac{17}{3},0 \right)\,\,and\,\,C\left( 3,8 \right).$
At, $A\left( 0,10 \right),Z=100(0)+120\left( 10 \right)=Rs.1200 $
$O(0,0), Z=100\left( 0 \right)+120\left( 0 \right)=Rs.0 $
$B\left( \dfrac{17}{3},0 \right),Z=100\left( \dfrac{17}{3} \right)+120\left( 0 \right)=Rs.566.67 $
$C\left( 3,8 \right),Z=100\left( 3 \right)+120\left( 8 \right)=Rs.1260 $
Thus, the maximum value of $Z=Rs.1260$ at x=3 and y=8.
Yes, the view of manufacturers that men and women workers are equally efficient is correct and so they should be paid at the same rate.

Hence, the answer is $Rs.1260$
Note: Alternate solution:
Let x units of A and y units of B be produced by the manufacturer. The price of one unit of A is Rs.100 and the price of one unit of B is Rs.120. Therefore, the total price of x units of A and y units of B or the total revenue is Rs. (100x + 120y).
$Z=100x+120y....\left( i \right)$
One unit of A requires 2 workers and one unit of B requires 3 workers. Therefore, x units of A and y units of B require (2x + 3y) workers. But the manufacturer has 30 workers. 2x + 3y s 30 workers
$2x+3y\le 30...\left( ii \right)$
Similarly, one unit of A requires 3 units of capital and one unit of B requires 1 unit of capital. Therefore, x units of A and y units of B require (3x + y) units of capital. But the manufacturer has 17 units of capital.
$3x+y\le 17...\left( iii \right)$
Thus, the given linear programming problem is
Maximize Z = 100x + 120y
subject to the constraints
\[\begin{align}
& \begin{array}{*{35}{l}}
2x\text{ }+\text{ }3y\text{ }\le \text{ }30 \\
3x\text{ }+\text{ }y\,\,\le \text{ }17 \\
\end{array} \\
&\Rightarrow x\ge 0...\left( iv \right) \\
&\Rightarrow y\ge 0...\left( v \right) \\
\end{align}\]
Now we will plot the graph on a plot of above constants or inequalities (ii),(iii),(iv), and (v). we get shaded regions as feasible regions having corner points A, O, B and C. The feasible region determined by the given constraints can be diagrammatically represented as

For the coordinates of C,
Two equations (ii) and (iii) are solved and we get coordinate of C = (3, 8)
Now, the value of Z is evaluated at the corner point as:
| Corner point | $Z=100x+120y$ |
| \[A\left( 0,\text{ }10 \right)\] | $1200$ |
| \[O\left( 0,\text{ }0 \right)\] | $0$ |
| $B\left( \dfrac{17}{3},0 \right)$ | $\dfrac{1700}{3}$ |
| $C\left( 3,8 \right)$ | $1260\leftarrow Maximum$ |
Therefore, maximum revenue is $Rs.1260$ when 2 workers and 8 units capital are used for production. Yes, although women workers have less physical efficiency but it can be managed by her other efficiency
Recently Updated Pages
Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Social Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Explain zero factorial class 11 maths CBSE

An example of chemosynthetic bacteria is A E coli B class 11 biology CBSE

State the laws of reflection of light

Name the metals and nonmetals in the first twenty class 11 chemistry CBSE

What is 1s 2s 2p 3s 3p class 11 chemistry CBSE




