Question

A man rows to a place 48 km distant and comes back in 48 hours. He finds that he can row 4 km with the stream at the same time as 3km against the stream. The rate of the stream is
[a] 0.5 km/hr
[b] 1 km/hr
[c] 3.5km/hr
[d] 1.8 km/hr.

Answer 1

Hint: Assume that the speed of the stream is x and the speed of the boat in still water is x. From the statement of the question form two equations in two variables x and y. This system is reducible to linear equations in two variables. Reduce the system to a system of linear equations in two variables by proper substitutions. Solve the system of equations using any one of the methods like Substitution method, elimination method, graphical method or using matrices. Hence find the value of x satisfying both the equation. The value of x will be the speed of the stream.

Complete step-by-step answer:
Let the speed of the stream be x, and the speed of the boat in still water be y.
We have the speed of the boat upstream = y-x.
Speed of the boat downstream = y+x.
Now since it takes 14 hours to reach a place at a distance of 48 km and come back, we have the sum of the times taken to reach the place downstream and time taken to return back upstream is equal to 14.
Now, we know that time $=\dfrac{\text{Distance}}{\text{speed}}$
Using, we get
Time taken to reach the place $=\dfrac{48}{y+x}$ and the time taken to return back $=\dfrac{48}{y-x}$.
Hence, we have
$\dfrac{48}{y+x}+\dfrac{48}{y-x}=14$
Dividing both sides by 2, we get
$\dfrac{24}{y+x}+\dfrac{24}{y-x}=7\text{ -----(i)}$
Also, the time taken to cover 4km downstream is equal to the time taken to cover 3km upstream.
Hence, we have $\dfrac{4}{y+x}=\dfrac{3}{y-x}$
Transposing the term on RHS to LHS, we get
$\dfrac{4}{y+x}-\dfrac{3}{y-x}=0\text{ -------- (ii)}$
Put $\dfrac{1}{y+x}=t$ and $\dfrac{1}{y-x}=u$, we have
$\begin{align}
  & 24t+24u=7\text{ -------(iii)} \\
 & \text{4}t-3u=0\text{ --------(iv)} \\
\end{align}$
Multiplying equation (iv) by 6 and subtracting from equation (iii), we get
$\begin{align}
  & 24t-24t+24u+18u=7 \\
 & \Rightarrow 42u=7 \\
\end{align}$
Dividing both sides by 42, we get
$u=\dfrac{7}{42}=\dfrac{1}{6}$
Substituting the value of u in equation (iv), we get
$\begin{align}
  & 4t-3\left( \dfrac{1}{6} \right)=0 \\
 & \Rightarrow 4t-\dfrac{1}{2}=0 \\
\end{align}$
Adding $\dfrac{1}{2}$ on both sides, we get
$4t=\dfrac{1}{2}$
Dividing both sides by 4, we get
$t=\dfrac{1}{8}$
Reverting to original variables, we have
$\dfrac{1}{y+x}=\dfrac{1}{8}$ and $\dfrac{1}{y-x}=\dfrac{1}{6}$
Taking reciprocals on both sides in both equations, we have
$\begin{align}
  & y+x=8\text{ ------- (v)} \\
 & y-x=6\text{ --------(vi)} \\
\end{align}$
Adding equation (v) and equation (vi), we get
$2y=14$
Dividing both sides by 2, we get
y=7.
Substituting the value of y in equation (v), we get
7+x=8
Subtracting 7 from both sides we get
x = 8-7 =1
Hence the speed of the stream is 1 km/hr.
Hence option [b] is correct.

Note: [1] Any system of type
 \[\begin{align}
  & {{a}_{1}}f\left( x,y \right)+{{b}_{1}}g\left( x,y \right)+{{c}_{1}}=0 \\
 & {{a}_{2}}f\left( x,y \right)+{{b}_{2}}g\left( x,y \right)+{{c}_{2}}=0 \\
\end{align}\]
is reducible to a system of linear equations in two variables by substituting f(x,y) =t and g(x,y) = u.
In the above question, we have $f\left( x,y \right)=\dfrac{1}{x+y}$ and $g\left( x,y \right)=\dfrac{1}{y-x}$.
[2] Graphically the curves $\dfrac{24}{y+x}+\dfrac{24}{y-x}=7$ and $\dfrac{4}{y+x}-\dfrac{3}{y-x}=0\text{ }$ will intersect each other at (7,1).

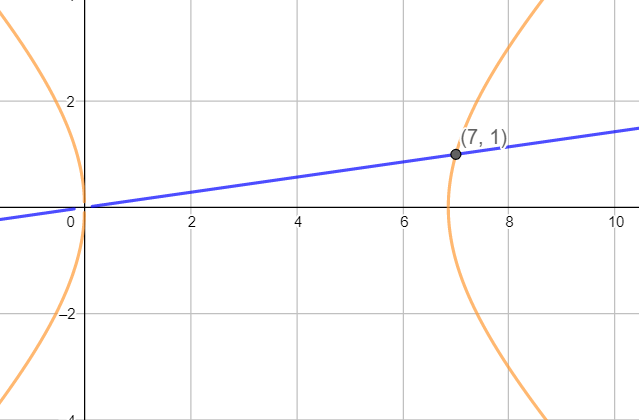
The orange curve is of equation (i) and the blue curve is of equation (ii).
It can be seen clearly that the lines intersect at (7,1).