Question

A man on the top of a cliff 100 m high, observe the angles of depression of two points on the opposite sides of the cliff as \[{{30}^{\circ }}\] and \[{{60}^{\circ }}\] respectively. Then, the distance between the two points is equal to
(a)$400\sqrt{3}m$
(b)$\dfrac{400}{\sqrt{3}}m$
(c)$\dfrac{100}{\sqrt{3}}m$
(d)$200\sqrt{3}$

Answer 1

Hint: For solving this problem, we consider two triangles ABD and ADC having respective bases as a and b in metres. Now, by applying the trigonometric ratio of $\tan \theta $ in both the triangles, we obtain the respective bases individually as height is already given in the problem statement. By adding both the bases of the triangle, we get the final answer.

Complete step-by-step answer:

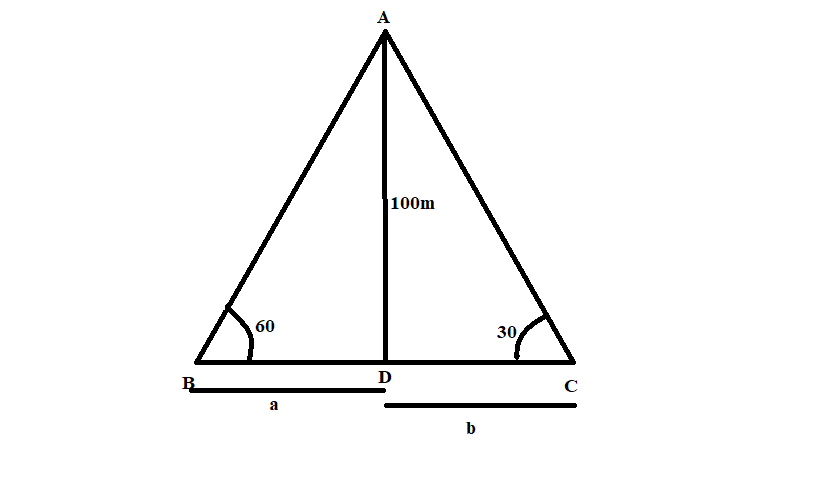
Let, the base of triangle ABD be ‘a’ meters and base of triangle ADC be ‘b’ meters.
According to the problem statement, the height of the cliff is 100m, $\angle ABD={{60}^{\circ }}$ and $\angle ACD={{30}^{\circ }}$.
One useful trigonometric ratio involved in this problem is tan which can be expressed as:
$\tan \theta =\dfrac{perpendicular}{base}$
In $\Delta ABD$, applying tan${{60}^{\circ }}$, we get
$\tan {{60}^{\circ }}=\dfrac{AD}{BD}$
As we know that the value of $\tan {{60}^{\circ }}=\sqrt{3}$, AD =100m and BD = a meter. Therefore, to evaluate a we put the values in the above ratio.
$\begin{align}
  & \sqrt{3}=\dfrac{100}{a} \\
 & a=\dfrac{100}{\sqrt{3}}m \\
\end{align}$
The length of BD is $\dfrac{100}{\sqrt{3}}m$.
In $\Delta ADC$, applying $\tan {{30}^{\circ }}$, we get
$\tan {{30}^{\circ }}=\dfrac{AD}{DC}$
As we know that the value of tan${{30}^{\circ }}=\dfrac{1}{\sqrt{3}}$, AD = 100 m and DC = b meter.
$\begin{align}
  & \dfrac{1}{\sqrt{3}}=\dfrac{100}{b} \\
 & b=100\sqrt{3}m \\
\end{align}$
The value of DC is $100\sqrt{3}m$,
Adding both the value of BD and DC with each other, we get
$\begin{align}
  & a+b=\dfrac{100}{\sqrt{3}}+100\sqrt{3} \\
 & a+b=\dfrac{400}{\sqrt{3}}m \\
\end{align}$
Hence, the distance between two points is $\dfrac{400}{\sqrt{3}}m$.
Therefore, option (b) is correct.
Note: The key concept involved in solving this problem is the knowledge of trigonometric ratio in the form of triangles. Once we know the value of angle subtended, we can easily find the ratio between the length by using tan operation.