Question

A man of mass 80 kg stands on a horizontal weighing machine of negligible mass, attached to a massless platform P that slides down at ${{37}^{\circ }}$ inclined. The weighing machine reads 72 kg. The man is always at rest w.r.t weighing machines. Calculate:
a. the vertical acceleration of the man.
b. the coefficient of kinetic friction $\mu $ between the platform and incline.

Answer 1

Hint: For the first part of the question, analyse the situation with respect to the platform. With respect to the platform, a pseudo force will be acting in the man. Figure out the net vertical force on man and use the given data about the weight weighed by the machine.

Formula used:
F=ma
$f=\mu N$

Complete step-by-step answer:
We will solve this question in two cases. Case 1 is to find the vertical acceleration of the man on the platform. Case 2 is to find the coefficient of kinetic friction between the platform and the incline.
We know that due to gravity the platform along with the man will accelerate downwards. However, the acceleration will be less than $g\sin 37$ because of the frictional force. Let the acceleration of the platform be a.

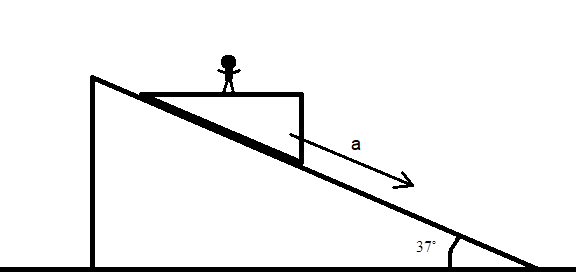
In case 1, let's consider the man and the platform. It is given that the man on the platform is at rest with respect to the platform. This means there is enough static friction between the man and the platform to keep him at with respect to the platform.
Let us analyse the case with respect to the platform. Since for the platform, the man is at rest, pseudo force will is acting on the man in the direction opposite to the direction of acceleration of the platform. This pseudo force will be equal to ma.
The weighing machine attached on the platform, will show the weight of the man by measuring the normal force exerted on it. Therefore, let us calculate the normal force exerted on the platform (weighing machine).
For this, resolve the force ma into its components, one in the direction along the horizontal and other along vertical. Let the horizontal force be $m{{a}_{x}}$ and the vertical force be $m{{a}_{y}}$as shown.

Here, ${{a}_{x}}=a\cos {{37}^{\circ }}$ and ${{a}_{y}}=a\sin {{37}^{\circ }}$
The net vertical force in the man is $mg-m{{a}_{y}}$, acting downwards. Therefore, the weighing machine will measure a force equal to $mg-m{{a}_{y}}$. However, it is given that the machine weighs the mass of the man as 72kg, which means that normal force on the machine is equal to 72g N.
Therefore, $mg-m{{a}_{y}}=72g$ ……(i).
Let us consider the value of g as $10m{{s}^{-2}}$.
Hence, we can write equation (i) as
$10m-m{{a}_{y}}=720$ and it is given that m=80kg.
$\Rightarrow 10\times 80-80{{a}_{y}}=720$
$\Rightarrow 80{{a}_{y}}=800-720\Rightarrow {{a}_{y}}=1m{{s}^{-2}}$.
Therefore, the vertical acceleration of the man is $1m{{s}^{-2}}$ downwards.
Since, ${{a}_{y}}=a\sin {{37}^{\circ }}$,
$a=\dfrac{{{a}_{y}}}{\sin {{37}^{\circ }}}=\dfrac{1}{\sin {{37}^{\circ }}}$.
$\sin {{37}^{\circ }}=\dfrac{3}{5}$
Therefore, $a=\dfrac{1}{\dfrac{3}{5}}=\dfrac{5}{3}m{{s}^{-2}}$.
This means the acceleration of the platform as well as the man is $\dfrac{5}{3}m{{s}^{-2}}$.
Now, let us deal with case 2.
Since the man and the platform have no relative motion, let us consider the two of them as a single body of mass 80kg sliding on a rough incline of angle ${{37}^{\circ }}$, with an acceleration of a. Let the coefficient of friction between the platform and the incline be $\mu $.
There will be two forces acting on this body. One is $mg\sin {{37}^{\circ }}$ and other is frictional force $\mu mg\cos {{37}^{\circ }}$, opposite to the direction of $mg\sin {{37}^{\circ }}$.
(Kinetic frictional force acting on a body is given as $\mu N$ and here $N=mg\cos {{37}^{\circ }}$).
Now if we draw the free body diagram of this body we get,

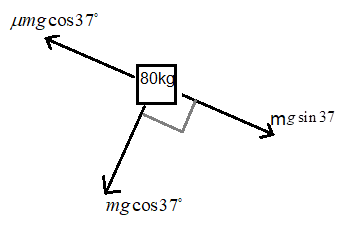
Therefore, the net force F acting on the body is $mg\sin {{37}^{\circ }}-\mu mg\cos {{37}^{\circ }}$.
But we also know that F=ma.
Hence, $F=mg\sin {{37}^{\circ }}-\mu mg\cos {{37}^{\circ }}=ma$ …..(ii).
Substitute the values of m, a, g and $\sin {{37}^{\circ }}$ in equation (ii).
Therefore,
$\left( 80 \right)\left( 10 \right)\left( \dfrac{3}{5} \right)-\mu \left( 80 \right)\left( 10 \right)\left( \dfrac{4}{5} \right)=\left( 80 \right)\left( \dfrac{5}{3} \right)$.
$\Rightarrow 6-8\mu =\left( \dfrac{5}{3} \right)$
Therefore,
$\mu =\dfrac{13}{24}$

Note: Remember, pseudo force is not a real force. Pseudo force comes into play when we change the frame of reference. Like in this case, the acceleration of the man with respect to the ground is a due to the component of force mg along the surface of the incline and the frictional force between the platform and the man.
However, with respect to the platform, the man is at rest. Hence, for the platform it seems as if there is a force (pseudo force) acting on the man that makes him to stay at rest.