Question

A man is standing on the deck of a ship which is 10 m above the water level. He observes the angle of elevation at the top of hill as $ {{60}^{\circ }} $ and angle of base of hill as $ {{30}^{\circ }} $ . Find the height of the hill from the base.

Answer 1

Hint: Here, we have to draw the figure with the given data. Let \[CD\]be the height of the hill. i.e.
\[CD\text{ }=\text{ }CE\text{ }+\text{ }ED\]. Consider $ \vartriangle ABC $ , calculate \[AE=BC\] by evaluating $ \tan {{30}^{\circ }} $ and then consider $ \vartriangle AED $ , calculate \[ED\] by evaluating $ \tan {{30}^{\circ }} $ . We have:
 $ \tan \theta =\dfrac{opposite\text{ }side}{adjacent\text{ }side} $

Complete step-by-step answer:
First we have to draw the figure with the given data.

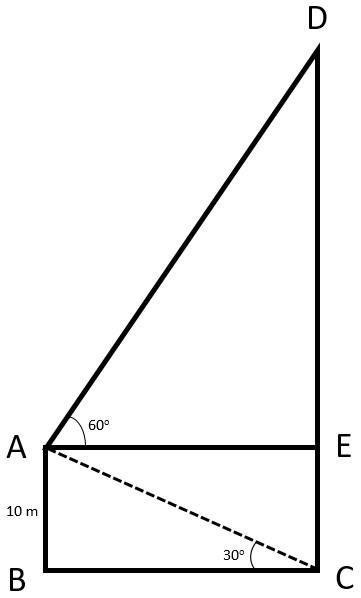
Here, given that a man standing at the deck of the ship is 10 m above the sea level. Also given that the angle of elevation at the top of the hill is $ {{60}^{\circ }} $ .The angle of depression at the base of hill is $ {{30}^{\circ }} $ .
Now, we have to calculate the height of the hill from the base.
We have \[AB=10m\]
The angle of elevation is , $ \angle EAD={{60}^{\circ }} $
The angle of depression is $ \angle BCA={{30}^{\circ }} $
Let \[CD\] be the height of the hill. From the figure we can say that:
\[CD=CE+ED\]
 First we have to find \[ED\]. For that consider the $ \vartriangle ABC $ ,
We know that,
 $ \tan \theta =\dfrac{opposite\text{ }side}{adjacent\text{ }side} $
 Therefore, we will get:
 $ \tan {{60}^{\circ }}=\dfrac{ED}{AE} $
We have $ \tan {{60}^{\circ }}=\sqrt{3} $ . Hence we will get :
 $ \sqrt{3}=\dfrac{ED}{AE} $
From the figure we can say that $ AE=BC $ . Hence we will obtain:
 $ \sqrt{3}=\dfrac{ED}{BC}\text{ }.....\text{ (1)} $
Now let us find $ BC $ for that consider $ \vartriangle ABC $ .
 $ \tan {{30}^{\circ }}=\dfrac{AB}{BC} $
We know that $ \tan {{30}^{\circ }}=\dfrac{1}{\sqrt{3}} $ , \[AB=10m\]. Therefore we will obtain:
 $ \dfrac{1}{\sqrt{3}}=\dfrac{10}{BC} $
 Now, by cross multiplication we get:
 $ BC=10\sqrt{3} $
Next, substitute the value $ BC=10\sqrt{3} $ in equation (1) we get:
 $ \sqrt{3}=\dfrac{ED}{10\sqrt{3}}\text{ } $
Now, by cross multiplication we get:
 $ \begin{align}
  & ED=10\sqrt{3}\times \sqrt{3} \\
 & ED=10\times 3 \\
 & ED=30 \\
\end{align} $
Next, we have to find $ CD $ where \[CD=CE+ED\]
We know that $ AB=CE=10m $ and $ ED=30 $ . Hence we get:
 $ \begin{align}
  & CD=10+30 \\
 & CD=40 \\
\end{align} $
 Therefore, we can say that the height of the hill from the base is $ 40m $.

Note: Here, instead of $ \vartriangle ABC $ you can also consider $ \vartriangle AEC $ since $ \angle BCA=\angle EAC={{30}^{\circ }} $ , i.e. they are alternate interior angles.