Question

A man is standing on the deck of a ship, which is 10m above the water level, observes the angle of elevation of the top of a hill as 60 degrees and the angle of depression of the base of the hill as 30 degrees. Find the distance of the hill from the ship and the height of the hill.

Answer 1

Hint: From the given question we can clearly see that it is based on the height and distance section of mathematics which includes depression, elevation and distance. Similarly, we are given all these situations using which we need to evaluate the distance of the hill from the ship including the height of the hill.

Complete step by step answer:
In the given question, we are provided with the information that the man is standing on the deck of the ship which is 10m above the sea level.
Now, the below is the figure of the given problem:

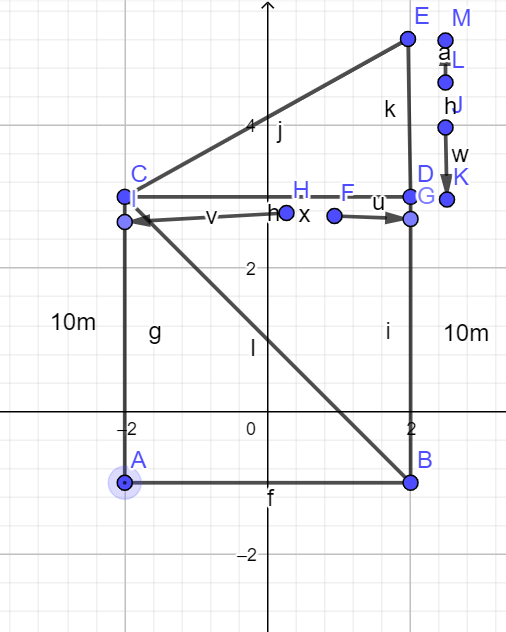
From the figure,
AC=10m
Let BE be the hill, then this implies CA=DB=10m
We are given that the angle of elevation to the top of the hill is ${{60}^{\circ }}$ ,
Therefore, from the triangle CDE,
$\tan {{60}^{\circ }}=\dfrac{h}{x}$
And this implies that
$\begin{align}
  & \sqrt{3}x=h \\
 & \Rightarrow x=\dfrac{h}{\sqrt{3}} \\
\end{align}$
Now, from the triangle BCD, we have
$\tan {{30}^{\circ }}=\dfrac{10}{x}$
And this implies that
$\begin{align}
  & \dfrac{1}{\sqrt{3}}=\dfrac{10}{x} \\
 & \Rightarrow x=10\sqrt{3} \\
\end{align}$
Now, after multiplying the two values of x we get,
${{x}^{2}}=10h$
$h=30m$
Therefore, the height of the hill is \[BE=BD+DE=10+30=40m\].
Therefore, the height of the hill is 40m and distance is $10\sqrt{3}$ .

Note: In these types of questions, we must make use of the figure which is drawn according to the given question and then proceed with the solution. Try to involve trigonometric functions in order to attain the missing values easily.