Question

A man can swim at the rate of \[5Km/hr\]in still water. A\[1Km\]wide river flows at the rate of \[3km/hr\].The man wishes to swim across the river directly opposite to the starting point.
a. Along what direction must the man swim?
b. What should be his resultant velocity?
c. How much time will he take to cross the river?

Answer 1

Hint: Initially direction of swim of man in still water is not taken perpendicular to the direction of river flow it should be taken at some angle from perpendicular direction of river flow so that when river will flow the velocity of man with respect to water change and he came across that direction so that he can swim directly opposite to starting point.

Complete step by step answer:

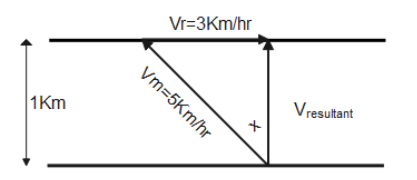
Let us suppose velocity of man with respect to water is V_m
\[{{V}_{m}}=5Km{{h}^{-1}}\] Let us suppose the width of the river is d. \[d=1Km\] Let us suppose velocity of the flow of river is V_r
\[{{V}_{r}}=3Km{{h}^{-1}}\]
a) A man wishes to swim across the river directly opposite to the starting point then he should flow at angle \[x\] with a perpendicular direction of river flow. So, direction in which man can swim is calculated as
 \[Sinx=\dfrac{{{V}_{r}}}{{{V}_{m}}}\]
\[\Rightarrow \]\[Sinx=\dfrac{3}{5}=0.6\]
\[\therefore \]\[x={{37}^{0}}\]
So man will swim at an angle of \[{{37}^{0}}\]with respect to the perpendicular direction of river flow.

b) Let us assume the resultant velocity as Vresultant._.
 In the given Triangle Apply Pythagoras theorem, we get
\[{{V}_{resul\tan t}}=\sqrt{{{V}_{m}}^{2}-{{V}_{w}}^{2}}\] \[\Rightarrow \]\[{{V}_{resul\tan t}}=\sqrt{{{5}^{2}}-{{3}^{2}}}\]
\[\therefore \]\[{{V}_{resul\tan t}}=4Km{{h}^{-1}}\](Direction perpendicular to river flow)

c) Let us assume time taken to cross the river directly is t.
So we get,
 \[t=\dfrac{Dis\tan ce}{Speed}=\dfrac{x}{{{V}_{resul\tan t}}}\]
\[\Rightarrow \]\[t=\dfrac{1}{4}hr\] \[\therefore \]\[t=15\min \]
ADDITIONAL INFORMATION: In river boat problem two cases are obtained-
1. A boat crosses the river in the shortest interval of time – To cross the river in the shortest interval of time, the boatman should steer his boat perpendicular to the river flow.
2. A boatman crosses the river covering the shortest distance – To cover the shortest distance means to reach the other end directly opposite to the starting point.

Note: Do not assume the direction of flow of man perpendicular to the direction of river flow because if he initially swims in the direction perpendicular to river flow then with the flow of river he is deviated from its original path and does not able to reach directly to opposite end from starting point.