Question

A man 6 feet tall casts a shadow 4 feet long at the same time when a flagpole casts a shadow 50 feet long. The height of the flag pole is:
$
  {\text{A}}{\text{. 80 ft}} \\
  {\text{B}}{\text{. 75 ft}} \\
  {\text{C}}{\text{. 60 ft}} \\
  {\text{D}}{\text{. 70 ft}} \\
$

Answer 1

Hint: In order to determine the height of the flagpole, we construct an appropriate figure representing all the data given in the question. We then use the property of similar triangles and establish a relation between the heights and shadows of both the man and the flag post. We solve this for an answer.

Complete step-by-step answer:
According to the data given in the question let us consider a figure that represents the heights and the shadows of both man and the flag post. It looks like two triangles as follows:

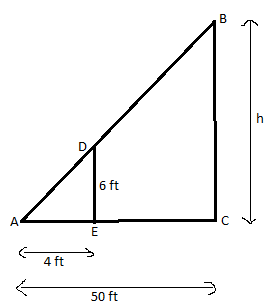
The height of the man is the side DE and his shadow is AE respectively. The height of the flag post is the side BC and its shadow is the side AC respectively. Both the man and the flag post are vertically upward from the ground.
Now by looking at the figure, we can say that ∆ADE and ∆ABC appear as two similar triangles. Therefore by using the property of corresponding sides of similar triangles we can say that the corresponding sides of both the triangles are in proportion.
Therefore we can say:
$ \Rightarrow \dfrac{{{\text{DE}}}}{{{\text{AE}}}} = \dfrac{{{\text{BC}}}}{{{\text{AC}}}}$
 $ \Rightarrow \dfrac{6}{4} = \dfrac{{\text{h}}}{{50}}$
$ \Rightarrow {\text{h = }}\dfrac{6}{4} \times 50$
⟹h = 75 feet.

Therefore the height of the flagpole is 75 feet.

Option B is the correct answer.

Note: In order to solve this type of question the key is to draw an appropriate figure which helps us identify the similar triangles the man and the flag post form.
It is important to know the concept of similar triangles to solve this type of problems. Similar triangles are those in which all the corresponding angles of both triangles are equal and the lengths of corresponding sides of both triangles are in equal ratio with each other.
In similar triangles, the ratio of areas of both triangles is proportional to the square of the ratio of lengths of their corresponding sides.
If the lengths of their corresponding sides are also equal then they are said to be congruent triangles.