Question

A long straight wire carries a current along the Z-axis. One can find two points in X-Y plane such that:
(This question has multiple correct options)
A. the magnetic fields are equal
B. the directions of the magnetic fields are the same
C. the magnitude of magnetic fields are equal
D. the field at one point is opposite to that at the other point

Answer 1

Hint:Use the formula for the magnetic field at a point near the current carrying conductor or a wire. Check on which quantity the magnetic field at a point near a wire carrying current depends. Hence, consider two points on the same side and either side of the wire and check the given options. Hence, determine the correct options.

Formula used:
The magnetic field \[B\] at a point near a current carrying conductor is
\[B = \dfrac{{{\mu _0}I}}{{2\pi d}}\] …… (1)
Here, \[{\mu _0}\] is magnetic permeability of free space, \[I\] is current in the conductor and \[d\] is the distance of the point from the conductor.

Complete step by step answer:
We have given that the direction of the current in a wire is along the Z-axis.

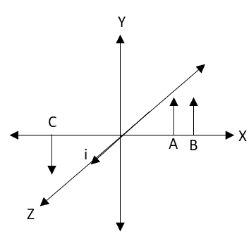
From equation (1), we can conclude that the magnetic field at a point near the current carrying wire depends only on the distance of that point from the wire as the current carrying from the wire is the same for all the points.

Let us consider points A and B on the same side of the current carrying wire at different distances from the wire.The magnitude of the magnetic field at points A and B is not the same as their distances from the wire are different. But according to right hand thumb rule, the directions of magnetic fields at these points A and B are the same in the upward direction.Therefore, we can have two points in the X-Y plane with same directions of the magnetic field but not the points for the magnetic field with the same magnitude and direction.Hence the option A is incorrect and the option B is correct.

Now let us consider two points B and C on the either sides of the wire at the same distance from the wire.The distance of the points B and C being the same from the wire, the magnitude of the magnetic field at points B and C is the same.Therefore, we can have two points in the X-Y plane with the same magnitude of the magnetic field.Hence, the option C is correct.

According to the right hand thumb rule, the direction of the magnetic field at point B is in upward direction and magnetic field at point C is in the downward direction.Therefore, we can have two points in the X-Y plane with different directions of the magnetic field.

Hence, the option D is correct.

Note:The students may think that the magnetic field for the two points on the same side of the current carrying wire should be the same as at both points the magnetic field is in the upward direction. But the magnetic field is a vector quantity which has both magnitude and direction. Here, at points A and B the magnitude of the magnetic field is different. Hence, the magnetic field at two points cannot be the same.