Question

A long horizontal rod has a bead which can slide along its length and is initially placed at a distance L from one end A of the rod. The rod starts from rest in angular motion about A with a constant angular acceleration $\alpha $. If the coefficient of friction between the rod and the bead is $\mu $ and gravity is neglected then what is the time after which the bead starts slipping?

Answer 1

Hint: The bead will start sliding when the centripetal force acting on the bead will become equal to the value of limiting friction. The limiting friction is the maximum value of friction. Motion will occur only if centripetal force can overcome this limiting friction.

Complete step by step answer:
When the rod is in an angular motion the bead is also moving in a circular path along with the rod.
Consider the figure below which shows the motion of the bead.

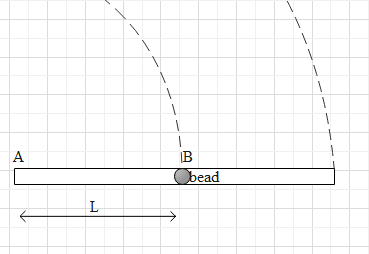
Let the angular velocity of the bead be $\omega $ and angular acceleration be $\alpha $.
The linear acceleration is the product of angular acceleration and the perpendicular distance.
$a = \alpha R$
Where $\alpha $ is the angular acceleration and $R$ is the radius.
Thus, linear acceleration of the bead will be,
$a = \alpha L$
The centripetal force is given as
${F_c} = \dfrac{{m{v^2}}}{R}$
$ \Rightarrow {F_c} = \dfrac{{m{v^2}}}{L}$
$ \Rightarrow {F_c} = \dfrac{{m{\omega ^2}{L^2}}}{L}$
 Since $\omega = \dfrac{v}{L}$
$\therefore {F_c} = m{\omega ^2}L$
When this centripetal force becomes equal to the value of maximum friction the bead will start to slide.
$ \Rightarrow {F_c} = {F_r}$ ----------(1)
We know that limiting friction is given as
${F_{\lim }} = \mu N$
Where $\mu $ is the coefficient of friction and N is the normal reaction.
Here, normal reaction $N$ is provided by the tangential force given as
${F_t} = ma$
On substituting the value of linear acceleration we get
$ \Rightarrow {F_t} = m\alpha L$
$\therefore N = m\alpha L$
Now substitute all the values in equation (1)
$ \Rightarrow m{\omega ^2}L = \mu m\alpha L$
$ \Rightarrow \omega = \sqrt {\mu \alpha } $ ----------- (2)
Now let us use the equation of motion.
$\omega = {\omega _0} + \alpha t$
Where, ${\omega _0}$ is the initial angular velocity, t is the time taken,$\alpha $is the angular acceleration.
It is given that it starts from rest. So, the initial angular velocity
${\omega _0} = 0$
$\therefore \omega = \alpha t$
$ \Rightarrow t = \dfrac{\omega }{\alpha }$
On substituting value of $\omega $ , we get
$ \Rightarrow t = \dfrac{{\sqrt {\mu \alpha } }}{\alpha }$
$ \Rightarrow t = \sqrt {\dfrac{\mu }{\alpha }} $

The time at which the bead will start sliding is $t = \sqrt {\dfrac{\mu }{\alpha }} $.

Note:
Remember that the limiting friction is the maximum value of friction. Motion will occur only if the force provided overcomes this maximum value.
Also, remember that gravity can be neglected. So, we did not take the effect of force due to gravity acting on the bead directly downwards. When gravity is present the weight of the bead $m\,g$ should also be taken into consideration.