Question

A line segment AM = a moves in the XOY plane such that AM is parallel to the X - axis.
If A moves along the circle ${{\text{x}}^2} + {{\text{y}}^2} = {{\text{a}}^2}$, then the locus of M is:
$
  {\text{A}}{\text{. }}{{\text{x}}^2} + {{\text{y}}^2} = {\text{4}}{{\text{a}}^2} \\
  {\text{B}}{\text{. }}{{\text{x}}^2} + {{\text{y}}^2} = 2{\text{ax}} \\
  {\text{C}}{\text{. }}{{\text{x}}^2} + {{\text{y}}^2} = 2{\text{ay}} \\
  {\text{D}}{\text{. }}{{\text{x}}^2} + {{\text{y}}^2} = 2{\text{ax + 2ay}} \\
$

Answer 1

Hint: In order to solve this question we make use of the given condition i.e. AM is parallel to the X-axis. We know the length of line segment AM, we make use of it to determine the locus of M using the equation of a circle given by,${\left( {{\text{x - a}}} \right)^2} + {\left( {{\text{y - b}}} \right)^2} = {{\text{r}}^2}$where a and b are the coordinates of a point on the circle and r is the radius.

Complete step-by-step answer:
Now given,
AM = a where AM is a line segment.
We construct a figure showing a circle with center O, with a point A (x, y) on it. AM is a line segment parallel to X – axis and let the coordinates of M be (α, β).

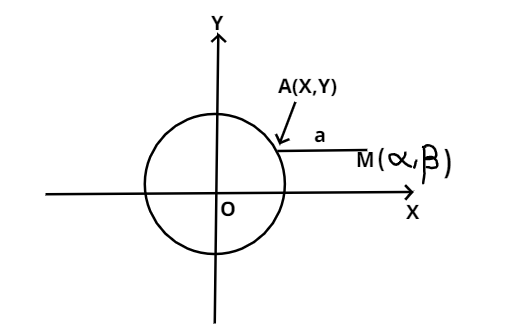
Now, let the coordinates of A be (x, y) and M be (α, β) as shown in figure.
Also given that AM is parallel to X - axis.

From the figure, we can write the coordinates of M as:
α = x + a and β = y
Or x = α – a and y = β
Also, given that this point A lies on the circle.

Therefore the coordinates of A must satisfy the equation of the circle.
$
  {\left( {\alpha - {\text{a}}} \right)^2} + {\beta ^2} = {{\text{a}}^2} \\
   \Rightarrow {\alpha ^2} - 2\alpha {\text{a + }}{\beta ^2} + {{\text{a}}^2} = {{\text{a}}^2} \\
  {\text{or }}{\alpha ^2} - 2\alpha {\text{a + }}{\beta ^2} = 0 \\
$
Now replace α with x and β with y we get,
 ${{\text{x}}^2} + {{\text{y}}^2} - 2{\text{ax = 0}}$
Therefore the locus of point M is
${{\text{x}}^2} + {{\text{y}}^2} = 2{\text{ax}}$
Therefore, the correct option is (B)

So, the correct answer is “Option B”.

Note: Whenever we face such types of questions the key concept is that we should assume the coordinates of points of line segment and then uses the given condition, like here it is given that the line segment is parallel to X-axis and then we find the values of assumed coordinates and then by putting them into the equation of the circle we get our desired equation of locus.