Question

A line cuts two sides \[AB\] and \[AC\] of \[\vartriangle ABC\] in points \[P\] and \[Q\],

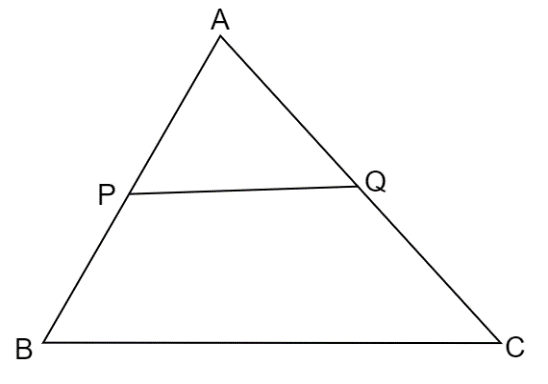
then prove \[\dfrac{{A\left( {\vartriangle APQ} \right)}}{{A\left( {\vartriangle ABC} \right)}} = \dfrac{{AP \cdot AQ}}{{AB \cdot AC}}\]

Answer 1

Hint: We will join \[B\] and \[Q\]. As we know, the ratio of areas of two triangles having equal height is equal to the ratio of their corresponding bases. Using this in \[\vartriangle APQ\] and \[\vartriangle ABQ\], we will find the ratio of sides \[AP\] and \[AB\] and in \[\vartriangle ABQ\] and \[\vartriangle ABC\], ratio of \[AQ\] and \[AC\]. Then we will multiply these two results to prove \[\dfrac{{A\left( {\vartriangle APQ} \right)}}{{A\left( {\vartriangle ABC} \right)}} = \dfrac{{AP \cdot AQ}}{{AB \cdot AC}}\].

Complete step by step solution:
We have to prove that the ratio of areas of \[\vartriangle APQ\] and \[\vartriangle ABQ\] is equal to \[\dfrac{{AP \cdot AQ}}{{AB \cdot AC}}\].
We will join \[B\] and \[Q\] to make \[BQ\] as shown in the figure below.

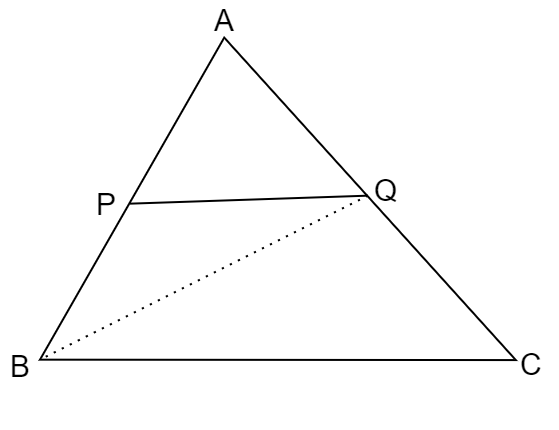
First consider \[\vartriangle APQ\] and \[\vartriangle ABQ\], as we know that the ratio of areas of two triangles having equal height is equal to the ratio of their corresponding bases. Using this, we can write that the ratio of area of \[\vartriangle APQ\] and area of \[\vartriangle ABQ\] is equal to the ratio of sides \[AP\] and \[AB\].
Therefore, we can write
\[ \Rightarrow \dfrac{{area\left( {\vartriangle APQ} \right)}}{{area\left( {\vartriangle ABQ} \right)}} = \dfrac{{AP}}{{AB}} - - - (1)\]
Now, consider \[\vartriangle ABQ\] and \[\vartriangle ABC\], as we know that the ratio of areas of two triangles having equal height is equal to the ratio of their corresponding bases. Using this, we can write that the ratio of area of \[\vartriangle ABQ\] and area of \[\vartriangle ABC\] is equal to the ratio of sides \[AQ\] and \[AC\].
Therefore, we can write
\[ \Rightarrow \dfrac{{area\left( {\vartriangle ABQ} \right)}}{{area\left( {\vartriangle ABC} \right)}} = \dfrac{{AQ}}{{AC}} - - - (2)\]
On multiplying \[(1)\] and \[(2)\], we get
\[ \Rightarrow \dfrac{{area\left( {\vartriangle APQ} \right)}}{{area\left( {\vartriangle ABQ} \right)}} \times \dfrac{{area\left( {\vartriangle ABQ} \right)}}{{area\left( {\vartriangle ABC} \right)}} = \dfrac{{AP}}{{AB}} \times \dfrac{{AQ}}{{AC}}\]
On simplification we get
\[ \Rightarrow \dfrac{{area\left( {\vartriangle APQ} \right)}}{{area\left( {\vartriangle ABC} \right)}} = \dfrac{{AP}}{{AB}} \times \dfrac{{AQ}}{{AC}}\]
On rewriting, we get
\[ \Rightarrow \dfrac{{A\left( {\vartriangle APQ} \right)}}{{A\left( {\vartriangle ABC} \right)}} = \dfrac{{AP \cdot AQ}}{{AB \cdot AC}}\]
Hence, proved that \[\dfrac{{A\left( {\vartriangle APQ} \right)}}{{A\left( {\vartriangle ABC} \right)}} = \dfrac{{AP \cdot AQ}}{{AB \cdot AC}}\].


Note:
Here, one important point to note is that we have proceeded the question according to the result we required. Construction that we have done, i.e., joining \[B\] and \[Q\] is also based on the result that is required. In other cases where we are required to prove some other result than we will do construction and we will apply the same method taking two different triangles accordingly.