Question

A light string passes over a frictionless pulley. To one of its ends a mass of 6kg is attached to the other end mass of 10kg is attached. The tension of the thread is
a) 24.5N
b) 2.45N
c) 79N
d) 73.5N

Answer 1

Hint: To calculate the tension in the thread we need to draw the free body diagram of the masses attached to the thread on the either side. Further we need to calculate the net force on each of the masses and obtain an expression for tension in the string. Tension in a string always acts opposite to the action of gravitational force on it.

Complete step-by-step solution:
To begin with let us first draw the free body diagram and obtain the net force on each of the masses.

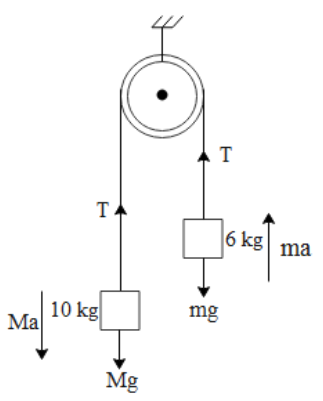
If we see the above free body diagram the mass M=10kg moves downwards, while the mass m=6kg moves upwards. Both of the masses move with common acceleration i.e. a. The net force on mass M is,
$Ma=Mg-T...(1)$ where g is the acceleration due to gravity and T is the tension in the rope. Similarly, the net force on m is given by, $ma=T-mg...(2)$ where g is the acceleration due to gravity and T is the tension in the rope. Dividing equation 1 by 2 we get,
$\begin{align}
  & \Rightarrow \dfrac{Ma}{ma}=\dfrac{Mg-T}{T-mg} \\
 & \Rightarrow \dfrac{M}{m}=\dfrac{Mg-T}{T-mg} \\
 & \Rightarrow MT-Mmg=mMg-Tm \\
 & \Rightarrow MT+Tm=mMg+Mmg \\
 & \Rightarrow T(M+m)=2mMg \\
 & \Rightarrow T=\dfrac{2mMg}{M+m} \\
\end{align}$
Hence from the above equation the tension in the thread across the pulley is,
$\begin{align}
  & \Rightarrow T=\dfrac{2mMg}{M+m} \\
 & \Rightarrow T=\dfrac{2\times 6\times 10\times 9.8}{10+6}=\dfrac{1176}{16}=73.5N \\
\end{align}$
Hence the correct answer is option d.

Note: It is to be noted that the above thread is assumed to be massless. Hence we can conclude that the tension at every point on the thread is constant. But in reality the thread also has mass, as a result the tension along the thread will be more at higher points from the point where the mass is attached to the thread.