Question

A light spring balance hangs from the hook of the other light spring balance and a block of mass M kg hangs from the former one. Then, the true statement about the scale reading is
 $ (A) $ Both the scales read $ M\text{ }kg $ each
 $ \left( B \right) $ The scale of the lower one reads $ M\text{ }kg $ and of the upper one zero.
 $ \left( C \right) $ The reading of the two scales can be anything but the sum of the readings will be $ M\text{ }kg $ .
 $ \left( D \right) $ Both the scales read $ M/2\text{ }kg $ .

Answer 1

Hint: Here we are given the data that two spring balances are hanging together provided that another mass block is hanging below the two spring balances. Let the upper spring balance be called $ S2 $ and lower spring balance be called $ S1 $ . We are also told that both the spring balances are light that means they are massless. So in order to solve this question we will use a simple concept of force that is net force acting on a system should be zero.

Complete step by step answer:
See the diagram for reference:

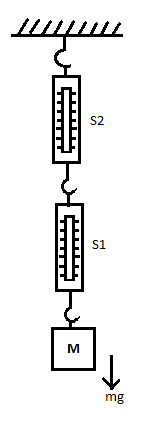
Now here the force acting on the mass block $ M $ is mg (its weight) in a downward direction. As both of the spring balances are massless then the reading of the lower spring balance will be $ S1 $ (due to mass block) and the reading of upper spring balance will be $ S2 $ (due to $ S1 $ and mass block). But spring balances are massless so the reading of both of the springs should be the same , that is M. Here, whatever force is experienced by $ S1 $ the same amount of force is experienced by $ S2 $ because the net force on the system should be zero. Therefore, $ S1=S2 $ . So when forces on both of the spring balances are equal then the reading will also be equal ( $ M\text{ }kg $ ).
Hence, option $ \left( A \right) $ is the correct option among all the given four options.

Note:
One has to note that if both of the spring balances were not massless and had some mass then reading on both of the spring balances would have been different, that is $ S1