Question

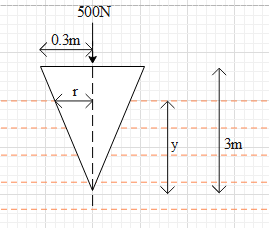
A light circular cone is pressed by a $ 500N $ force as shown in figure then the path depth up to which it will submerged is ( $ g = 10m{s^{ - 2}} $ )

(A) $ 1.16m $
(B) $ 2.0m $
(C) $ 2.1m $
(D) $ 3.0m $

Answer 1

Hint :This question involves the concept of buoyancy. Find the force of buoyancy exerted by the liquid on the cone and equate it to the applied force externally. You can find the depth to which the cone is submerged by using the formula for the volume of a cone.
 $ {F_B} = \rho g{V_s} $ , where $ {F_B} $ is the buoyant force applied by a liquid of density $ \rho $ when a volume of $ {V_s} $ is submerged in the liquid. $ g $ is acceleration due to gravity.

Complete Step By Step Answer:
Let us assume that the cone is inside water.
It is given that the cone is being pressed and some part of it is submerged under water. Also, the cone is pressed with a force of $ 500N $ in the downward direction.
Since the cone is light, we can ignore the gravitational force acting on it.
And since the cone is submerged in water, the water will exact buoyant force on the cone, in the upward direction. This buoyant force will balance the force by which the cone is pressed.
The buoyant force on the cone is equal to $ {F_B} = \rho g{V_s} $ …. $ \left( i \right) $
From the figure we can see that the shape of the submerged volume is also a cone of radius $ r $ and height $ y $ .
Therefore,
 $ {V_s} = \pi {r^2}y $ …. $ \left( {ii} \right) $

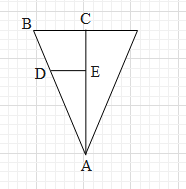
From the figure we also get that $ \Delta ABC \approx \Delta ADE $ (similar triangles).
From the properties of similar triangles we get that $ \dfrac{r}{{0.3}} = \dfrac{y}{3} $
 $ \Rightarrow r = \dfrac{y}{{10}} $
Substitute this value in $ \left( {ii} \right) $
 $ \Rightarrow {V_s} = \pi {\left( {\dfrac{y}{{10}}} \right)^2}(y) = \pi \dfrac{{{y^3}}}{{100}} $
Now, substitute this value in $ \left( i \right) $
 $ \Rightarrow {F_B} = \rho g{V_s} = \rho g\pi \dfrac{{{y^3}}}{{100}} $
Density of water is $ \rho = 1000kg{m^{ - 3}} $ .
 $ \Rightarrow {F_B} = \rho g\pi \dfrac{{{y^3}}}{{100}} = (1000)(10)\pi \dfrac{{{y^3}}}{{100}} $
 $ \Rightarrow {F_B} = 100\pi {y^3} $
Since, the buoyant force balances the applied force we can write that $ {F_B} = 500N $ .
 $ \Rightarrow 500 = 100\pi {y^3} $
 $ \Rightarrow {y^3} = \dfrac{5}{\pi } $
 $ \Rightarrow y = {\left( {\dfrac{4}{\pi }} \right)^{1/3}} = 1.16m $
Hence, the correct option is A.

Note :
Here, it is important to understand the buoyancy which is exerted by the water to that of the object submerged in that water. If the force is exerted externally on the object immersed in water then the force or buoyant force exerting on the object by water is equal and opposite. Buoyant force acts like an opposing force.