Question

A lens has a convex surface one side and a concave surface another side. If the radius of curvature of convex and concave are equal to R each and µ is refractive index of lens then its focal length is:
$\begin{align}
  & A.\text{ }\dfrac{2R}{\mu -1} \\
 & B.\text{ }\dfrac{R}{2\left( \mu -1 \right)} \\
 & \text{C}\text{. zero} \\
 & \text{D}\text{. infinite} \\
\end{align}$

Answer 1

Hint: Question has been provided with a lens which is made up of convex surface and concave surface. To find the focal length of a given lens, use lens formula which will give the relation between refractive index of lens, refractive index of surrounding, curvature of surface and focal length. Put value of respective quantity and get value for focal length of lens.
Formula used:
By lens maker formula.
$\dfrac{1}{f}=\left( \dfrac{{{\mu }_{2}}}{{{\mu }_{1}}}-1 \right)\left( \dfrac{1}{{{R}_{1}}}-\dfrac{1}{{{R}_{2}}} \right)$
Where, ${{\mu }_{1}}$ = refractive index of surrounding medium
${{\mu }_{2}}$ = refractive index of thin glass lens
${{R}_{1}}$ = radius of curvature of convex lens
${{R}_{2}}$ = radius of curvature of concave lens
F = focal length of lens

Complete answer:

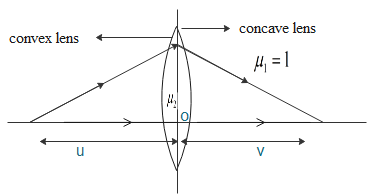
As shown in figure a lens has formed by using convex surface and concave surface. Consider On one side and another side respectively. Now we need to find out the focal length of a given lens.
$\dfrac{1}{f}=\left( \dfrac{{{\mu }_{2}}}{{{\mu }_{1}}}-1 \right)\left( \dfrac{1}{{{R}_{1}}}-\dfrac{1}{{{R}_{2}}} \right)......\left( 1 \right)$
In the question it has given that curvature of both the lens is R. Let ${{\mu }_{2}}=\mu $ be the refractive index of lens formed from convex and concave mirror (shown in figure) and let ${{\mu }_{1}}=1$ be the refractive index of air i.e. surrounding medium of lens.
Then equation (1) can be written as,
$\begin{align}
  & \dfrac{1}{f}=\left( {{\mu }_{2}}-1 \right)\left( \dfrac{1}{{{R}_{1}}}-\dfrac{1}{{{R}_{2}}} \right) \\
 & \therefore \dfrac{1}{f}=\left( \mu -1 \right)\left( \dfrac{1}{R}-\dfrac{1}{R} \right) \\
 & \therefore \dfrac{1}{f}=\left( \mu -1 \right)\left( 0 \right) \\
 & \therefore \dfrac{1}{f}=0 \\
 & \therefore f=\infty \\
\end{align}$
Hence, focal length of the lens is infinity.

Therefore the correct option is (D).

Additional Information:
The formula showing the relation between focal length (f) distance of object (u) and distance of image (v) is known as lens formula which is given as,
$\dfrac{1}{f}=\dfrac{1}{v}-\dfrac{1}{u}$
The lens formula is the same for any spherical lens and any distance of the object from the lens.it is however necessary to use the sign convention properly. According to Cartesian sign convention, the optical center (O) is taken to be the origin. Consider the principal axis in the x-axis of frame of reference. The sign convention is given as follows.
1) The object will always be placed on the left of the lens. All distances parallel to the principal axis are measured from the optical center (O).
2) Distance measured on the right side of the lens will be taken as positive whereas distance measured on the left side of the lens will be taken as negative.
3) Distance perpendicular to the principal axis and above it will be taken as positive while below it is taken as negative.
4) Focal length of convex lens will be positive while that of convex lens will be taken as negative.

Note:
Lens maker formula is given in equation formula is applicable only when the surrounding medium will be air. If the object is at infinity then its image is formed at the focal point. I.e. if $u=\infty $ then v=f then lens maker formula is
$\dfrac{1}{f}=\left( \dfrac{{{\mu }_{2}}}{{{\mu }_{1}}}-1 \right)\left( \dfrac{1}{{{R}_{1}}}-\dfrac{1}{{{R}_{2}}} \right)$
If thin lens are dipped in water or any other medium then focal length of lens will be change lens of any desired focal length can be produced by choosing proper values of ${{R}_{1}},\text{ }{{R}_{2}},\text{ }{{\mu }_{1}}\text{ }and\text{ }{{\mu }_{2}}$.