Question

A lamp standing at a point A on a circular path of radius \[r\] subtends an angle \[\alpha \]at some point B on the path, and AB subtends an angle of \[{45^ \circ }\] at any other point on the path, the height of the lamp post is

Answer 1

Hint:
Trigonometry is a branch of Mathematics that Studies Relationships between Side lengths and angles of triangles. The field emerged in the Hellenistic world during the century BC from applications century to astronomical studies. In trigonometry we study about trigonometric functions i.e. sine, cosec, tangent, cot, sec, cosec. In practical, mostly the trigonometry is used to make the roof of the building inclined, and to measure the angles etc.…
In Trigonometry Basic and mostly used formulae are:
\[\sin \theta = \dfrac{{Perpendicular}}{{Hypotenuse}}\],\[\cot \theta = \dfrac{{Base}}{{Perpendicular}}\]
\[\cos \theta = \dfrac{{Base}}{{Hypotenuse}}\],\[\sec\theta = \dfrac{{Hypotenuse}}{{Base}}\]
\[\tan \theta = \dfrac{{Perpendicular}}{{Base}}\],\[\cos ec\theta = \dfrac{{Hypotenuse}}{{Perpendicular}}\]
These Hypotenuse Perpendicular and the Base are subjected to the triangle.
And \[\sin \theta ,\cos \theta ,\tan \theta \] are Reciprocals of \[\cos ec\theta\ ,\sec \theta\ ,\cot \theta \]

Complete step by step solution:

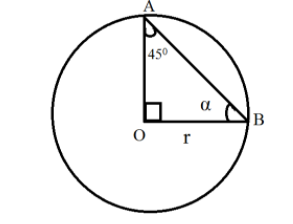
O is the center; r is the radius. ‘B’ subtends \[\alpha \] on the path, ‘AB’ subtends \[{45^0}\] on the path.
Since AB subtends an angle of \[{45^ \circ }\] at any point on the circle.
Therefore, it subtends an angle of \[{90^ \circ }\] at the center.
\[\therefore \] According to Hypotenuse Theorem
\[\mathop {(hypotenuse)}\nolimits^2 = \mathop {(perpendicular)}\nolimits^2 + \mathop {(base)}\nolimits^2 \]
Since, the triangle is \[{90^ \circ }\]
\[\therefore \] Perpendicular \[ = \] Base \[ = \] r.
Now, \[AB = \sqrt {\mathop r\nolimits^2 + \mathop r\nolimits^2 } \]
\[ = r\sqrt 2 \]
Since, \[\tan \theta = \dfrac{{Perpendicular}}{{Base}}\]
\[\therefore \,\tan \alpha = \dfrac{h}{{AB}}\] (According to the Question)
\[\tan \alpha = \dfrac{h}{{r\sqrt 2 }}\]\[ \Rightarrow \,h = r\sqrt 2 \,\tan \alpha \]

Note:
Since trigonometry has a limited set of rules, formulae and the method so there will be no alternate method. Since we used \['\tan \alpha '\] in case of that we can also use \['\cot \theta '\] which is B Perpend.