Question

A ladder rests against a wall at an angle \[\alpha \] to the horizontal. Its foot is pulled away from the wall through a distance a slides a distance b down the wall making an angle \[\beta \] with the horizontal. Choose the correct option-
(a) \[a=b\tan \left( \dfrac{\alpha +\beta }{2} \right)\]
(b) \[b=a\tan \left( \dfrac{\alpha +\beta }{2} \right)\]
(c) \[a=b\sin \left( \dfrac{\alpha +\beta }{2} \right)\]
(d) \[b=a\sin \left( \dfrac{\alpha +\beta }{2} \right)\]

Answer 1

Hint: In this question, first draw the diagram it will give us a clear picture of what we have to find out. Then from the triangles so formed in the diagram apply the tangent formula and then get the relation between the distance and the angles. Now, simplify it further to get the relation given in the options

\[\sin \theta =\dfrac{\text{Opposite}}{\text{Hypotenuse}}\]

\[\cos \theta =\dfrac{\text{adjacent}}{\text{Hypotenuse}}\]


Complete step-by-step answer:
Let us first draw the diagram with the given conditions.

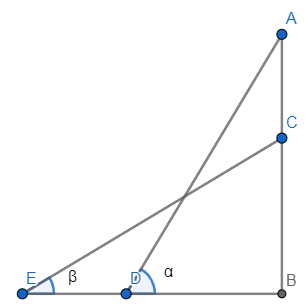
Given, in the question that ED is a and AC is b.

Now, let us assume the length of the ladder as l.

Also assume that BD as x and BC as h.

Let us first consider the triangle BDA.

Now, using the sine formula we can write that.

\[\begin{align}
  & \Rightarrow \sin \alpha =\dfrac{b+h}{l} \\
 & \Rightarrow l\sin \alpha =b+h.........\left( 1 \right) \\
\end{align}\]

Now, let us consider the triangle BEC.

Here, by applying the sine formula again we get,

\[\begin{align}
  & \Rightarrow \sin \beta =\dfrac{h}{l} \\
 & \Rightarrow l\sin \beta =h............\left( 2 \right) \\
\end{align}\]

Now, on subtracting the equations (1) and (2) we get,

\[\Rightarrow b=l\left( \sin \alpha -\sin \beta \right).........\left( 3 \right)\]

Again from the triangle BDA on applying the cosine formula this time we get,

\[\begin{align}
  & \Rightarrow \cos \alpha =\dfrac{x}{l} \\
 & \Rightarrow l\cos \alpha =x.........\left( 4 \right) \\
\end{align}\]

Now, again considering the other triangle BEC and then applying the cosine formula we get,

\[\begin{align}
  & \Rightarrow \cos \beta =\dfrac{a+x}{l} \\
 & \Rightarrow l\cos \beta =a+x............\left( 5 \right) \\
\end{align}\]

Let us now subtract the equations (4) and (5) then we get,

\[\Rightarrow a=l\left( \cos \beta -\cos \alpha \right).........\left( 6 \right)\]

Let us now divide the equations (3) and (6) and solve them further.

\[\Rightarrow \dfrac{a}{b}=\dfrac{\cos \beta -\cos \alpha }{\sin \alpha -\sin \beta }\]

Now, by using the transformation formula we can further simplify it as:

\[\Rightarrow \dfrac{a}{b}=\dfrac{2\sin \left( \dfrac{\alpha +\beta }{2} \right)\sin \left(
\dfrac{\alpha -\beta }{2} \right)}{2\cos \left( \dfrac{\alpha +\beta }{2} \right)\sin \left(
\dfrac{\alpha -\beta }{2} \right)}\]

\[\left[ \begin{align}
  & \because \cos C-\cos D=2\sin \left( \dfrac{C+D}{2} \right)\sin \left( \dfrac{D-C}{2} \right) \\
 & \sin C-\sin D=2\cos \left( \dfrac{C+D}{2} \right)\sin \left( \dfrac{C-D}{2} \right) \\
\end{align} \right]\]

\[\begin{align}
  & \Rightarrow \dfrac{a}{b}=\dfrac{\sin \left( \dfrac{\alpha +\beta }{2} \right)}{\cos \left( \dfrac{\alpha +\beta }{2} \right)} \\
 & \Rightarrow \dfrac{a}{b}=\tan \left( \dfrac{\alpha +\beta }{2} \right)\text{ }\left[ \because \tan \theta =\dfrac{\sin \theta }{\cos \theta } \right] \\
\end{align}\]

\[\therefore a=b\tan \left( \dfrac{\alpha +\beta }{2} \right)\]

Hence, the correct option is (a).

Note: Instead of applying the sine formula and the cosine formula to both the triangles and then subtracting them to write in the form of a and b. We can directly apply the tangent formula to both the triangles and then simplify it using the half angle formula which in turn we can directly get the result in terms of tangent but it will be lengthy.
While applying the sine formula and cosine formula we need to cross check the values of opposite, adjacent and hypotenuse sides because interchanging any of the terms will not give the proper equation. Then while applying the transformation formula we need to apply the corresponding formula with the respective signs of the angles.