
A ladder $9{\text{m}}$ long reaches a point $9{\text{m}}$ below the top of a vertical flagstaff. From the foot of the ladder, the elevation of the flagstaff is ${60^ \circ }$. What is the height of the flagstaff?
A.$9{\text{m}}$
B.$10.5{\text{m}}$
C.$13.5{\text{m}}$
D.$15{\text{m}}$
Answer
579.3k+ views
Hint: Here, the total length of the flagstaff (BC) will be the sum of the length from the top of the flagstaff to the point $9{\text{m}}$ below the top of a vertical flagstaff (DC) and the length below this point (BD). So here since the angle of elevation is bisected by the ladder in half then $\angle BAD = {30^ \circ }$. Then use the sine ratio $\sin \theta = \dfrac{P}{H}$ where P is perpendicular and H is hypotenuse in triangle ABD to find the value of BD and then add it to CD to get the answer.
Complete step-by-step answer:
Let AD be the ladder whose length=$9{\text{m}}$ and it reaches at point D which is $9{\text{m}}$below the top of a vertical flagstaff BC. It is given that $\angle BAC = {60^ \circ }$ which means $\angle BAD = \angle CAD = {30^ \circ }$
We have to find BC. Let BD=h cm so we can say that BC=BC+DC-- (i)
Now we have to find BD.
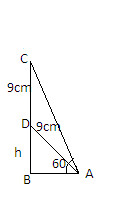
In triangle ABD, $\sin \theta = \dfrac{{BD}}{{AD}}$ because we know that $\sin \theta = \dfrac{P}{H}$ where P is perpendicular and H is hypotenuse.
On putting the given values, we get-
$ \Rightarrow \sin {30^ \circ } = \dfrac{h}{9}$
We know that $\sin {30^ \circ } = \dfrac{1}{2}$
So on putting this value, we get-
$ \Rightarrow \dfrac{1}{2} = \dfrac{h}{9}$
On rearranging, we get-
$ \Rightarrow h = \dfrac{9}{2} = 4.5$m
On putting this value and value of CD in eq. (i), we get-
$ \Rightarrow $ BC=$4.5 + 9 = 13.5$ m
The correct answer is option C.
Note: Here, in triangle ABD we have not taken the angle as $\cos \theta $ or $\tan \theta $ because in both their ratios the base comes in the denominator, and in triangle ABD, we do not know the value of the base AB.
Here $\cos \theta = \dfrac{B}{H} = \dfrac{{AB}}{{AD}}$ but here we do not know the value of AB and we have to find BC which cannot be found using this.
When we are solving such a question, we always use the angle which can be used to find the unknown value using the known value like- here in the question, we have used the known value (AD) to get the value of BD.
Complete step-by-step answer:
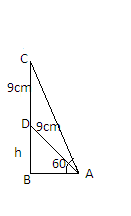
Let AD be the ladder whose length=$9{\text{m}}$ and it reaches at point D which is $9{\text{m}}$below the top of a vertical flagstaff BC. It is given that $\angle BAC = {60^ \circ }$ which means $\angle BAD = \angle CAD = {30^ \circ }$
We have to find BC. Let BD=h cm so we can say that BC=BC+DC-- (i)
Now we have to find BD.

In triangle ABD, $\sin \theta = \dfrac{{BD}}{{AD}}$ because we know that $\sin \theta = \dfrac{P}{H}$ where P is perpendicular and H is hypotenuse.
On putting the given values, we get-
$ \Rightarrow \sin {30^ \circ } = \dfrac{h}{9}$
We know that $\sin {30^ \circ } = \dfrac{1}{2}$
So on putting this value, we get-
$ \Rightarrow \dfrac{1}{2} = \dfrac{h}{9}$
On rearranging, we get-
$ \Rightarrow h = \dfrac{9}{2} = 4.5$m
On putting this value and value of CD in eq. (i), we get-
$ \Rightarrow $ BC=$4.5 + 9 = 13.5$ m
The correct answer is option C.
Note: Here, in triangle ABD we have not taken the angle as $\cos \theta $ or $\tan \theta $ because in both their ratios the base comes in the denominator, and in triangle ABD, we do not know the value of the base AB.

Here $\cos \theta = \dfrac{B}{H} = \dfrac{{AB}}{{AD}}$ but here we do not know the value of AB and we have to find BC which cannot be found using this.
When we are solving such a question, we always use the angle which can be used to find the unknown value using the known value like- here in the question, we have used the known value (AD) to get the value of BD.
Recently Updated Pages
Basicity of sulphurous acid and sulphuric acid are

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Computer Science: Engaging Questions & Answers for Success

Class 10 Question and Answer - Your Ultimate Solutions Guide

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Trending doubts
Who is known as the "Little Master" in Indian cricket history?

Explain the Treaty of Vienna of 1815 class 10 social science CBSE

A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

Which are the three major ports of Tamil Nadu A Chennai class 10 social science CBSE

The highest dam in India is A Bhakra dam B Tehri dam class 10 social science CBSE

Describe the process of Unification of Italy class 10 social science CBSE




