Question

A ladder $25m$ long just reaches the top of the building $24m$ high from the ground. Find the distance of the foot of the ladder from the building.

Answer 1

Hint:
First we need to figure out from the given data. We get the shape of a right angled triangle. For a right angled triangle we can apply Pythagoras theorem. Applying Pythagoras theorem we can find the distance of the foot of the ladder from the building.

Complete step by step solution:

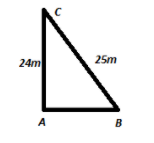
$BC$ be the ladder which $25m$ long
 $AC$ be the height of the building which heights is $24m$
$AB$ be the distance between the ladder and the building
Now we need to find the distance of the foot of the ladder from the building which means we have to find the value of$AB$ .
As we know it is a right angled triangle we can apply Pythagoras theorem
Now what is Pythagoras theorem says,
Pythagoras theorem says that in a right angled triangle the sum of the squares of the two right angle sides will always be the same as the square of the hypotenuse.
The statement gives that $B{{C}^{2}}=A{{B}^{2}}+A{{C}^{2}}$
Here hypotenuse side is $BC$
Two right angle sides are$AB$ ,$AC$
We need to find the $AB$ value so take $AB$ in one side we get,
$\Rightarrow A{{B}^{2}}=B{{C}^{2}}-A{{C}^{2}}$
Apply the value into this
$\Rightarrow A{{B}^{2}}={{25}^{2}}-{{24}^{2}}$
Squaring these values we get
$\Rightarrow A{{B}^{2}}=625-576$
Subtract these two numbers we get
$\Rightarrow A{{B}^{2}}=49$
Take the square to opposite side it will become square root to the number
$\Rightarrow AB=\sqrt{49}$
We can write $49$ as multiples of $7\times 7$
$\Rightarrow AB=\sqrt{7\times 7}$
When we take a num out from the square root we can take one number
So we get,
$\Rightarrow AB=7m$

The distance of the foot of the ladder from the building is $7m$.

Note:
This method can also apply to equilateral triangle and isosceles right triangle. If two straight lines are given, the Pythagorean theorem allows us to calculate the length of the diagonal connecting them.