Question

A ladder $20ft$ long reaches a point $20ft$ below the top of a flag. The angle of elevation of the top of the flag at the foot of the ladder is ${60^ \circ }$. Find the height of the flag.

Answer 1

Hint: We are given the length of ladder, that means hypotenuse length is given to us. And let if the height of the flag be $h$, then the height where the ladder meets from ground will be $\left( {h - 20} \right)ft$. Let $a$ be the horizontal distance between the point and the foot of the flag. Angle of elevation is given as ${60^ \circ }$. You will get two equations to solve it and you will get your answer.

Complete step-by-step answer:
We are given that a ladder is of length $20ft$. Since the ladder represents the slant length which reaches the point below $20ft$ from the top of the flag.
So, let the height of the flag be $h$ and the distance from foot of ladder to foot of flag be $x$.
               

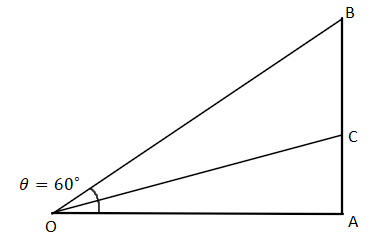
Here let $AB$ be the height of the flag, that means $AB = h$.
And $OC$ be the ladder whose length is given that is $OC = 20ft$.
Now, the ladder meets at $C$ which is $20ft$ below the top of the flag. So, $BC = 20ft$.
And we let $\angle AOB$ be $\theta $.
Here, $\theta $ represents the angle of elevation which is given ${60^ \circ }$.
Hence, $\theta = {60^ \circ }$
Now, we assume length $OA = b$.
Let $\angle AOC = \alpha $
Now, in $\vartriangle OBC$, we know that
$OC = 20ft$ as given in the question.
And also, it is given $BC = 20ft$.
So, $OC = BC$
Hence, it is an isosceles triangle.
We know the angles opposite to equal sides are equal.
Hence, equal sides are $OC{\text{ and }}BC$.
Therefore, $\angle OBC = \angle COB$
We can write
$
  \angle COB = \angle AOB - \angle AOC \\
  \angle COB = 60 - \alpha \\
 $
So, $\angle OBC = 60 - \alpha $
Now, we know that $\vartriangle AOB$ is a right angled triangle with $\angle A = {90^ \circ }$.
We know that sum of angles$ = {180^ \circ }$
So,
$
  \angle A + \angle AOB + \angle OBA = {180^ \circ } \\
  90 + 60 + 60 - \alpha = 180 \\
  \alpha = 210 - 180 = {30^ \circ } \\
  {\text{So, we got }}\angle OBC = 60 - 30 = {30^ \circ } \\
  {\text{And }}\angle AOC = {30^ \circ } \\
 $
Now, in $\vartriangle AOC$
We know
$
  AC = AB - BC \\
  AC = \left( {h - 20} \right)ft \\
  {\text{And }}OC = 20ft \\
 $
And also, we found that $\angle AOC = {30^ \circ }$
So,
$
  \sin \angle AOC = \dfrac{{{\text{perpendicular}}}}{{{\text{hypotenuse}}}} = \dfrac{{AC}}{{OC}} \\
  \sin {30^ \circ } = \dfrac{{h - 20}}{{20}} \\
  {\text{We know }}\sin {30^ \circ } = \dfrac{1}{2} \\
   \Rightarrow \dfrac{1}{2} = \dfrac{{h - 20}}{{20}} \\
  10 = h - 20 \\
  h = 30ft \\
 $
So, the height of the flag is $30ft$.

Note: In the right- angle triangle, only you can use this property of $\sin \theta = \dfrac{{{\text{perpendicular}}}}{{{\text{hypotenuse}}}}$.
But, for any triangle, you can use sine formula
$\dfrac{{\sin A}}{a} = \dfrac{{\sin B}}{b} = \dfrac{{\sin C}}{c}$ where $a,b,c$ are the sides opposite to the angles $\angle A,\angle B,\angle C$ respectively.