Question

A ladder 20 meters long reaches a point 20 meters below the top of the flag. If the angle of elevation of the top of the flag at the foot of the ladder is \[{{60}^{\circ }}\], the length of the flagstaff, in meters is
A.. 40
B.. 20
C.. 30
D.. \[10\left( 2+\sqrt{3} \right)\]

Answer 1

Hint:In this question, it is given that there is a ladder leaning against a flagstaff such that the part of flagstaff above the point of contact, between the ladder and flagstaff, is 20 meters in height till the top of the flag. The angle of elevation of the top of the flag from the foot of the ladder is \[{{60}^{\circ }}\] and we have to find the full length of the flagstaff. There is a formation of 2 triangles with the same base with one of the vertices on the foot of the ladder and both are right-angled triangles, so we can apply trigonometric functions in them. First, we will apply the tangent trigonometric function in a bigger triangle and we will end up with a relation between the base length and the full length of the flagstaff or perpendicular of the triangle and then we will apply the Pythagoras theorem in the smaller triangle and substitute the base length in terms of perpendicular length calculated from a larger triangle.

Complete step by step answer:
In this question, it is given that a ladder of length 20 meters is leaning against a flagstaff such that the point of contact between the flagstaff and the ladder is 20 meters below the top of the flagstaff where there is a flag at the top.

Now there is the formation of a right-angled triangle in which the ladder is acting as the hypotenuse of length 20 meters, the length of the flagstaff from the ground till the point of contact is to be assumed as \[x\] and is acting as perpendicular and the base is from the foot of ladder till the foot of flagstaff and it will be represented by \[B\].

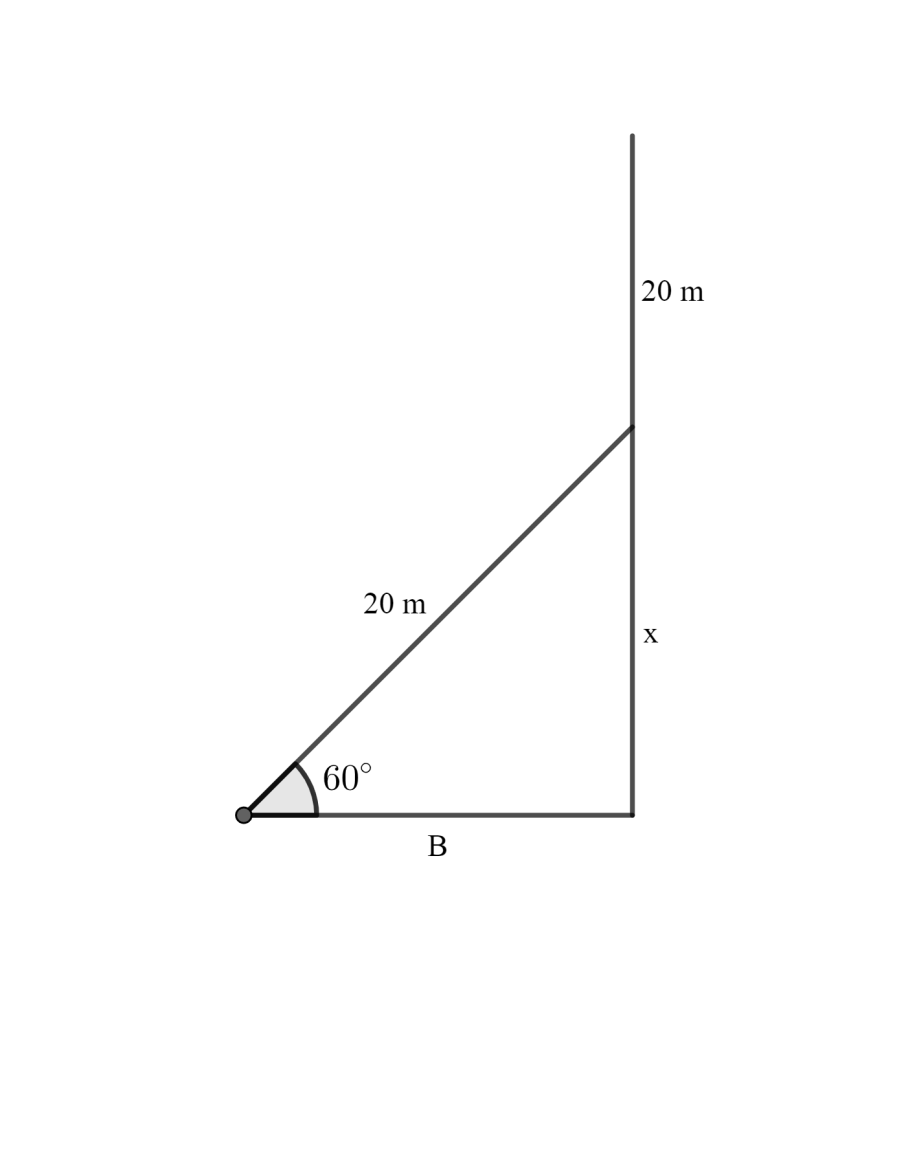
Now, we will be applying the trigonometric functions we will use: sine function to find out the value of x
Now, we know that:
\[\sin \theta =\dfrac{perpendicular}{Hypotenuse}\]
\[\sin {{60}^{\circ }}=\dfrac{x}{20}\]
\[\dfrac{\sqrt{3}}{2}=\dfrac{x}{20}\]
Now we will get the value of $x$, as follows:
\[x=\dfrac{\sqrt{3}\times 20}{2}\Rightarrow x=10\sqrt{3}\]
Now, as we can see from the figure the total length of flagstaff will be $\left( 20+x \right)$ , therefore the length of flagstaff will be: $20+x=20+10\sqrt{3}\Rightarrow 10\left( 2+\sqrt{3} \right)$
Hence option D is the answer.
Note:
 Always remember to apply trigonometric function in a right-angled triangle there should either be given at least an angle and one side or at least two sides to evaluate other elements of the triangle otherwise it is of no use. In these questions always draw figures to get the idea of the approach to solve the question, just focus on what is to be found and what relates it to the given quantities then the question will become easy and the figure will let you analyze the situation properly.