Question

A ladder 17m long reaches a window of a building 15m above the ground. Find the distance of the foot of the ladder from the building.

Answer 1

Hint: In order to solve this problem, we need to assume that the angle made by building with the ground is ${{90}^{\circ }}$ . Therefore, we can use Pythagoras theorem. The Pythagoras theorem says that ${{\left( \text{Hypotenuse} \right)}^{\text{2}}}\text{=}{{\left( \text{Side}\,\text{1} \right)}^{\text{2}}}\text{+}{{\left( \text{Side}\,\text{2} \right)}^{\text{2}}}$ where the hypotenuse is the side opposite to the right angle.

Complete step by step answer:
We are given that there is a window of the building 15m high. And we have a ladder that is 17m tall in order to reach the window.
We have to make the following assumptions,
We have to assume that the building is straight with respect to the wall. The angle made by building with the ground is ${{90}^{\circ }}$ .
Let the distance of the foot of the ladder from the building be $x\,m.$
We can interpret the question more with the help of a diagram.

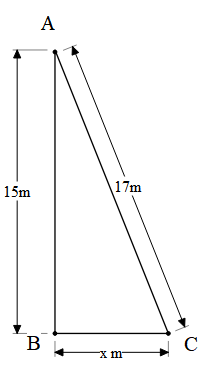
We can see that AB is the distance of the window from the wall, AC is the length of the ladder.
And BC is the segment we need to find.
As we have assumed, $\angle ABC={{90}^{\circ }}$ , we can use the Pythagoras theorem.
Pythagoras theorem is only applicable for right-angle triangles.
It says that, ${{\left( \text{Hypotenuse} \right)}^{\text{2}}}\text{=}{{\left( \text{Side}\,\text{1} \right)}^{\text{2}}}\text{+}{{\left( \text{Side}\,\text{2} \right)}^{\text{2}}}$, where the hypotenuse is the side opposite to ${{90}^{\circ }}$ .
We know that hypotenuse = AC ,side 1 = AB, side 2 = BC,
By substituting the values, we get that,
$\begin{align}
  & {{\left( AC \right)}^{2}}={{\left( AB \right)}^{2}}+{{\left( AC \right)}^{2}} \\
 & \Rightarrow {{\left( 17 \right)}^{2}}={{\left( 15 \right)}^{2}}+{{\left( x \right)}^{2}} \\
\end{align}$
Solving for x we get,
${{x}^{2}}={{17}^{2}}-{{15}^{2}}=64$
Taking the square root and neglecting the negative sign, we get,
$x=\sqrt{64}=8m$ .
Therefore, the distance of the foot of the ladder from the building is 8m.

Note: We can easily look for hypotenuse as hypotenuse is the largest side in the right angle triangle. We also need to make the important assumption that the building is at the right angle with the ground. Without this assumption, we cannot use the Pythagoras theorem. We are ignoring the negative root of x because x is the distance and it can never be negative.