Question

A ladder 17 m long reaches the window of a building 15 m above the ground. Find the distance of the foot of the ladder from the building.
A). 8 m
B). 5 m
C). 10 m
D). 12 m

Answer 1

Hint: In this question it is given that a ladder(AC) 17 m long reaches the window(A) of a building(AB) 15 m above the ground. We have to find the distance of the foot of the ladder from the building, i.e the length of BC.

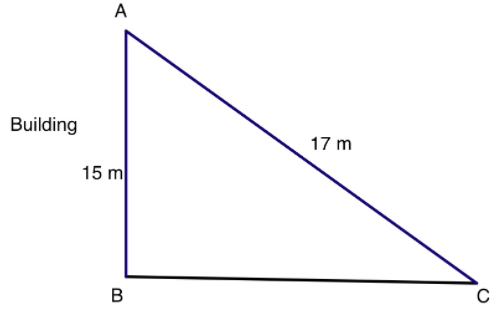
Since the above triangle is forming a right angle triangle, where base is BC, height is AB and the hypotenuse is AC. So to find the distance BC, we need to use the Pythagorean theorem.

Complete step-by-step solution:
Let us consider the height of the window from the foot of the building to be AB, which is given 15 m. And the ladder AC which is 17 m.
i.e, AB = 15 m and AC = 17 m.
Now by Pythagorean theorem we can write,
$$\left( \text{Height} \right)^{2} +\left( \text{Base} \right)^{2} =\left( \text{Hypotenuse} \right)^{2} $$
$$\Rightarrow \left( AB\right)^{2} +\left( BC\right)^{2} =\left( AC\right)^{2} $$
Now by putting the values we get,
$$\left( 15\right)^{2} +\left( BC\right)^{2} =\left( 17\right)^{2} $$
$$\Rightarrow (15\times 15)+\left( BC\right)^{2} =(17\times 17)$$ [$$\because a^{2}=a\times a$$]
$$\Rightarrow 225+\left( BC\right)^{2} =289$$
$$\Rightarrow \left( BC\right)^{2} =289-225$$ [by changing the side]
$$\Rightarrow \left( BC\right)^{2} =64$$
$$\Rightarrow BC=\sqrt{64}$$
$$\Rightarrow BC=\sqrt{8\times 8}$$
$$\Rightarrow BC=8$$ [$$\because \sqrt{a\times a} =a$$]
Therefore the distance of the foot of the ladder from the building is 8 m.
Hence the correct option is option A.

Note: While solving this type of question you need to know that the pythagorean theorem always applies on a right angle triangle. So Pythagorean theorem states that the summation of the squares of the base and height is equal to the square of hypotenuse,
i.e $$\left( \text{Height} \right)^{2} +\left( \text{Base} \right)^{2} =\left( \text{Hypotenuse} \right)^{2} $$