Question

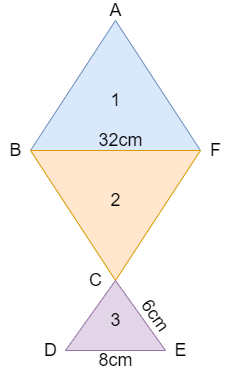
A kite is in the shape of a square with a diagonal of \[32cm\] and an isosceles triangle of base \[8cm\] and sides \[6cm\] each is to be made of three different shades as shown in the figure. How much paper of each shade has been used in it?

Answer 1

Hint: We solve this problem simply by using the formula of area of triangle given as
_{\[A=\dfrac{1}{2}\left( \text{Base} \right)\left( \text{Height} \right)\]}
For a square we know that the diagonal divides the square into two parts of equal area. So, the areas of part 1 and part 2 are equal. For finding the side length of square we use the Pythagoras theorem which states that the square of hypotenuse is equal to sum of squares of other two sides that is for the triangle shown below

The Pythagoras theorem is given as \[{{b}^{2}}={{a}^{2}}+{{c}^{2}}\].
Also for finding the height of the triangle we use the condition the height of the isosceles triangle will be the median.by using the above conditions we find areas of each part.

Complete step by step answer:
Let us find the area of part 1 first
(i) Area of part 1
Let us assume that the triangle \[\Delta ABF\] in different orientation as follows

We know that the all sides of square are equal so, let us assume that
\[\Rightarrow BA=AF=a\]
We are given that the length of diagonal as \[32cm\] so, we have
\[\Rightarrow BF=32cm\]
We know that the Pythagoras theorem which states that the square of hypotenuse is equal to sum of squares of other two sides that is for the triangle shown below

The Pythagoras theorem is given as\[{{b}^{2}}={{a}^{2}}+{{c}^{2}}\].
By using the above theorem to triangle \[\Delta ABF\] we get
\[\Rightarrow B{{A}^{2}}+A{{F}^{2}}=B{{F}^{2}}\]
By substituting the required values we get
\[\begin{align}
  & \Rightarrow {{a}^{2}}+{{a}^{2}}={{32}^{2}} \\
 & \Rightarrow 2{{a}^{2}}=1024 \\
 & \Rightarrow a=\sqrt{512}=16\sqrt{2}cm \\
\end{align}\]
Let us assume that the area of part 1 as \[{{A}_{1}}\]
We know that the formula of area of triangle as
\[\Rightarrow A=\dfrac{1}{2}\left( \text{base} \right)\left( \text{height} \right)\]
By using the above formula to \[\Delta ABF\] we get
\[\Rightarrow {{A}_{1}}=\dfrac{1}{2}\left( a \right)\left( a \right)=\dfrac{{{a}^{2}}}{2}\]
By substituting the required values in above equation we get
\[\begin{align}
  & \Rightarrow {{A}_{1}}=\dfrac{{{\left( 16\sqrt{2} \right)}^{2}}}{2} \\
 & \Rightarrow {{A}_{1}}=\dfrac{512}{2}=256c{{m}^{2}} \\
\end{align}\]

Therefore the area of part 1 is \[256c{{m}^{2}}\]
Now, let us solve the second part.
(i) Area of part 2
Let us assume that the area of part 2 as \[{{A}_{2}}\]
We know that the diagonal of a square divides the square into two triangles of same area that is
\[\Rightarrow {{A}_{2}}={{A}_{1}}=256c{{m}^{2}}\]
Therefore the area of part 2 is \[256c{{m}^{2}}\]
(iii) Area of part 3
Let us take the triangle \[\Delta CDE\] and draw the height as shown below.

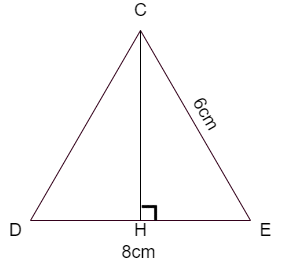
We are given that the dimensions of each triangle are \[8cm,6cm,6cm\]
So, from the triangle \[\Delta CDE\] we have
\[\begin{align}
  & \Rightarrow CE=CD=6cm \\
 & \Rightarrow DE=8cm \\
\end{align}\]
We know that the altitude of isosceles triangle will be the median
So, the point ‘H’ is mid – point of ‘DE’
So, we can the length of ‘HE’ as
\[\begin{align}
  & \Rightarrow HE=\dfrac{DE}{2} \\
 & \Rightarrow HE=\dfrac{8cm}{2}=4cm \\
\end{align}\]
We know that the Pythagoras theorem states that the square of hypotenuse is equal to sum of squares of other two sides that is for the triangle shown below

The Pythagoras theorem is given as \[{{b}^{2}}={{a}^{2}}+{{c}^{2}}\].
By using the above theorem to triangle \[\Delta CHE\] we get
\[\Rightarrow C{{H}^{2}}+H{{E}^{2}}=C{{E}^{2}}\]
Now by substituting the required values in above equation we get
\[\begin{align}
  & \Rightarrow C{{H}^{2}}+{{4}^{2}}={{8}^{2}} \\
 & \Rightarrow C{{H}^{2}}=64-16 \\
 & \Rightarrow CH=\sqrt{48}=4\sqrt{3}cm \\
\end{align}\]
Now, we know that the area formula of triangle is given as
\[A=\dfrac{1}{2}\left( \text{Base} \right)\left( \text{Height} \right)\]
Let us assume that the area of triangle \[\Delta CDE\] as \['{{A}_{3}}'\]
Then by using the area formula we get
\[\Rightarrow {{A}_{3}}=\dfrac{1}{2}\left( DE \right)\left( CH \right)\]
Now, by substituting the required values in above equation we get
\[\begin{align}
  & \Rightarrow {{A}_{3}}=\dfrac{1}{2}\left( 8cm \right)\left( 4\sqrt{3}cm \right) \\
 & \Rightarrow {{A}_{3}}=16\sqrt{3}c{{m}^{2}} \\
\end{align}\]

Therefore the area of third part is \[16\sqrt{3}c{{m}^{2}}\].

Note: We have shortcut to solve the area of part 1 and part 2
Let us assume that the area of square \[ABCF\] as \['A'\]
We are given that the diagonal of square as \[32cm\]
We know that the area formula of square having the diagonal as \['d'\] is given as
\[\Rightarrow A=\dfrac{1}{2}{{d}^{2}}\]
By substituting the required values in above formula we get
\[\begin{align}
  & \Rightarrow A=\dfrac{1}{2}{{\left( 32 \right)}^{2}} \\
 & \Rightarrow A=512c{{m}^{2}} \\
\end{align}\]
The area of square is sum of areas of part 1 and part 2 that is
\[\Rightarrow {{A}_{1}}+{{A}_{2}}=A\]
We know that the diagonal divides the square into two triangles of same area so, we have
\[\Rightarrow {{A}_{1}}={{A}_{2}}\]
By substituting this result in above equation we get
\[\begin{align}
  & \Rightarrow 2{{A}_{1}}=512c{{m}^{2}} \\
 & \Rightarrow {{A}_{1}}={{A}_{2}}=256c{{m}^{2}} \\
\end{align}\]
Therefore the areas of part 1 and part 2 are \[256c{{m}^{2}}\]