Question

A kite is flying at a height of 75 m from the ground level, attached to a string inclined at $60^o$ to the horizontal. Find the length of the string to the nearest metre.

Answer 1

Hint: The angle of elevation is the angle above the eye level of the observer towards a given point. The angle of depression is the angle below the eye level of the observer towards a given point. The sine function is the ratio of the opposite side and the hypotenuse.

Complete step-by-step answer:

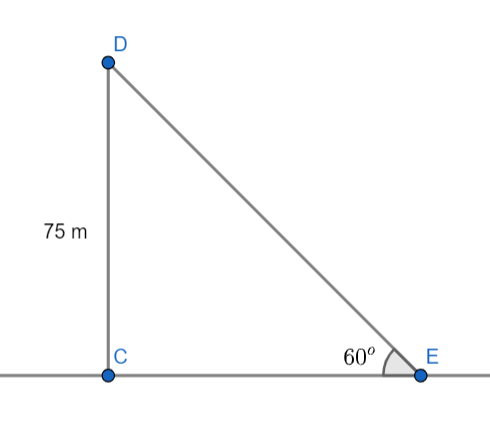
Let the string DE be of the length x. The height of the kite CD is 75 m. It is given that the wire ED makes an angle of $60^o$ with the horizontal. We will apply trigonometric formulas in triangle DCE as follows-

$

  In\;\vartriangle DCE,\; \\

  \sin {60^{\text{o}}} = \dfrac{{CD}}{{ED}} \\

  \dfrac{{\sqrt 3 }}{2} = \dfrac{{75}}{{\text{x}}} \\

  {\text{x}} = 75 \times \dfrac{{\sqrt 3 }}{2} = 64.95 \approx 65\;{\text{m}} \\

$

This is the length of the string to the nearest metre, which is the required answer.


Note: In such types of questions, it is important to read the language of the question carefully and draw the diagram step by step correctly. When the diagram is drawn, we just have to apply basic trigonometry to find the required answer.