Question

A kettle with 2-litre water at $27^{\circ} C$ is heated by an operating coil heater of power $1kW$. The heat is lost to the atmosphere at a constant rate of $160 J/sec$ when its lid is open. In how much time will water be heated to $77^{\circ} C$ with the lid open? (specific heat of water= 4.0 kJ/kg)

Answer 1

Hint: According to the law of conservation of energy, the heat lost by a hot body is completely absorbed by a cold body. This flow of heat continues until the two bodies are in thermal equilibrium. This is known as the principle of calorimetry.

Complete step by step solution:

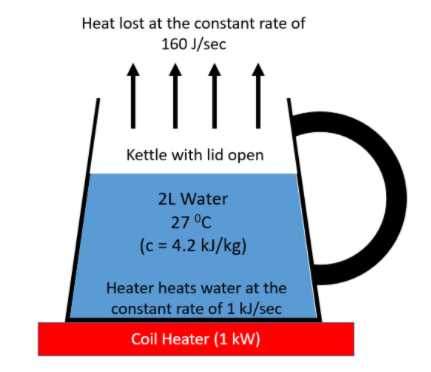
As seen in the diagram, there is a kettle with its lid open and containing $2$ litres of water at $27^{\circ} C$. The kettle is kept on a coil heater of power $1 kW$. This means the heater is capable of heating at a constant rate of $1 kJ/sec$ or $1000 J/sec$. Since the lid is open, the water loses heat at a constant rate of $160 J/sec$ as mentioned in the question.
Let us assume at a certain time $T$, the heater heats the water inside the kettle to a temperature of $77^{\circ} C$. Therefore, the heat energy supplied by the coil heater until time $T$ is
${{E}_{heater}}=(1000T\,)\,J$ ………. (1)
The water in the kettle absorbs the heat supplied by the heater. At time T, the water gets heated up and attains a temperature of $77^{\circ} C$. Therefore, heat energy absorbed by the water until time $T$ is given by
${{E}_{water}}=m\times c\times \Delta \theta $ ………. (2)
Where $m$ is the mass of water present in the kettle, $c$ is the specific heat capacity of water, and $\Delta\theta$ is the change in temperature of water (i.e. initial temperature subtracted from the final temperature).
Mass of water can be expressed in terms of volume and density as
$m=V\times \rho $ ………. (3)
Here, $\rho$ is the density of water, which is 1 kg/L. Therefore
$\begin{align}
  & m=(2\times 1)\,kg \\
 & m=2\,kg
\end{align}$
Now, substituting the values of m, c, and $\Delta\theta$ in Eq. 2, we get
$\begin{align}
  & {{E}_{water}}=2\times 4.2\times {{10}^{3}}\times (77-27) \\
 & {{E}_{water}}=42\times {{10}^{4}}\,J \\
\end{align}$
Heat lost due to open lid until time T is
${{E}_{lost}}=160T$ ………. (4)
Now, by the law of conservation of energy, energy supplied by the heater until time T must be equal to the sum of energy absorbed by water and energy lost due to the absence of lid. Therefore,
$\begin{align}
  & {{E}_{heater}}={{E}_{water}}+{{E}_{lost}} \\
 & \Rightarrow 1000T=42\times {{10}^{4}}+160T \\
 & \Rightarrow 840T=42\times {{10}^{4}} \\
 & \Rightarrow T=500\,\sec \\
 & \Rightarrow T=8\,\min \,20\,\sec \\
\end{align}$

$\therefore$ The heater will take $8 \text{ minutes } 20 \text{ seconds }$ to heat the water to $77^{\circ} C$.

Note:
In this question, the specific heat capacity of the material of the kettle was neglected. In the former case, the kettle will also absorb heat supplied from the heater and has to be considered while performing the calculations.