Question

A joker’s cap is in the form of a right circular cone of base radius \[7\]cm and height \[24\]cm. Find the area of the sheet required to make \[10\] such caps.

Answer 1

Hint: Basic formula for finding total surface area of a right circular cone will be used. Also, since it’s a right circular cone therefore, we will use Pythagoras Theorem to calculate slant height of the cone.

Complete step-by-step answer:
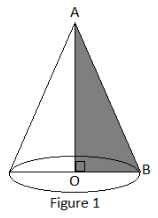
Consider the figure \[1\], length of line segment AO is \[24\]cm and that of OB is \[7\]cm. The line segments AO and OB represents the height and radius of the joker’s cap. The line segment AB represents slant height of the cone.

Total surface area of a cone is equal to the sum of its curved surface area and the base area. Its formula is given as,
Total surface area of a cone \[{{\pi r}}\left( {{\text{l}} + {\text{r}}} \right)\], where l is the slant height of the cone.
In order to calculate T.S.A. of joker’s cap, we must first calculate its slant height.
 Using Pythagoras theorem in triangle AOB right angled at O,
\[
{\left( {{\text{AO}}} \right)^2} + {\left( {{\text{OB}}} \right)^2} = {\left( {{\text{AB}}} \right)^2}
{\left( {24} \right)^2} + {\left( 7 \right)^2} = {\left( {{\text{AB}}} \right)^2} \\
576 + 49 = {\left( {{\text{AB}}} \right)^2} \\
625 = {\left( {{\text{AB}}} \right)^2}
\]
It is clear from the above calculation that slant height is equal to \[25\]cm.
Now, we will substitute the given and calculated values of radius, height and slant height in the T.S.A. formula, we obtain,
\[
{\text{T}}{\text{.S}}{\text{.A}}{\text{.}} = {{\pi r}}\left( {{\text{l}} + {\text{r}}} \right) \\
= \pi \times 7\left( {25 + 7} \right) \\
= \dfrac{{22}}{7} \times 7\left( {32} \right) \\
= 704
 \]
So, from the above calculation we observe that the total surface area of the cone is \[704\;{\text{c}}{{\text{m}}^2}\]. Now, in the question we are asked to find the area of sheet required to make \[10\] such caps, therefore, we will multiply total surface area of one cap by \[10\] i.e., \[10 \times 704 = 7040\,{\text{c}}{{\text{m}}^2}\].

Hence, the area of the sheet required to make \[10\] such caps is \[7040\,{\text{c}}{{\text{m}}^2}\].

Note: In such types of problems, it is important to recall basic formulas of area, volume, total surface area of geometric figures. Also, the concept of unitary method must be clear and in such problems it should be applied definitely. Construction of figure and its labelling should be done in the first step only to get proper visualization of the given mathematical object so that area, volume or any other physical quantity could be computed accurately.