Question

A horizontal platform with an object placed on it executing SHM in the vertical direction. The amplitude of oscillation $3.29 \times {10^{ - 3}}m,$ What must be the least period of these oscillations, so that the object is not detached from the platform?
A. $0.1256\sec $
B. $0.1356\sec $
C. $0.1456\sec $
D. $0.1556\sec $

Answer 1

Hint: The object will not detach from the horizontal platform if the downward acceleration of the platform is equal to the acceleration due to gravity.
$a = {w^2}A$
$T = \dfrac{{2\pi }}{w}$

Complete step by step answer:

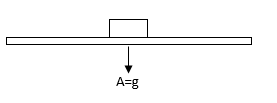
It is given in the question that,
A horizontal platform is executing SHM in a vertical direction. An object is placed on the horizontal platform.
Now, when the platform is in downward motion, at that time.
If acceleration of the platform is greater than the acceleration due to gravity. Then the platform will come down at a faster rate than the object as the object will be coming down by the pull of acceleration due to gravity.
Thus, the object will detach from the platform.
Therefore, if the object is not to be detached from the platform, the acceleration of the horizontal surface should be equal to the acceleration due to gravity.
So, that the platform and the object to come down with the same force and do not get detached.
We know that
$a = {w^2}A$
Where,$a$is acceleration
$w$is angular velocity
$A$is the amplitude of oscillation.
$ \Rightarrow {a_{\max }} = {w^2}_{\max }A$ . . . (1)
Where, ${a_{\max }}$ and ${w_{\max }}$ are maximum acceleration and maximum angular velocity, represented.
As we discussed,
${a_{\max }} = g$ . . . (2)
Where, $g$ is acceleration due to gravity.
From equation (1) and (2), we get
$g = {w^2}_{\max }A$
Re – arranging it, we get
${w^2}_{\max } = \dfrac{g}{A}$
By taking square root, we get
 ${w^2}_{\max } = \sqrt {\dfrac{g}{A}} $ . . . (3)
Now, we know that,
Time period, $T$ is given by
$T = \dfrac{{2\pi }}{w}$
Now, $T$ is minimum it is maximum
\[ \Rightarrow {T_{\min }} = \dfrac{{2\pi }}{{{w_{\max }}}}\]
By substituting the value from equation (3), we get
\[ \Rightarrow {T_{\min }} = \dfrac{{2\pi }}{{{w_{\max }}}}\]
$ = 2\pi \sqrt {\dfrac{A}{g}} $
By substituting in given values in it, we get
${T_{\min }} = 2\pi \sqrt {\dfrac{{3.29 \times {{10}^{ - 3}}}}{{10}}} (\because g \approx 10m/s)$
$ = 2 \times 3.14\sqrt {3.29 \times {{10}^{ - 4}}} $
$ = 6.28 \times 1.81 \times {10^{ - 2}}$
$ = 11.39 \times {10^{ - 2}}$
 \[{T_{\min }} = 0.113\sec \]

So, the correct answer is “Option A”.

Note:
We could calculate the value of ${T_{\min }}$ by log table.
Or we could also calculate is by approximation, for example,
${T_{\min }} = 2 \times 3.14\sqrt {3.29 \times {{10}^{ - 4}}} $
Write $3.14 \approx 3.29 \approx 3$
$ \Rightarrow {T_{\min }} = 2 \times 3.14\sqrt 3 \times {10^{ - 2}}$
$ = 6 \times 1.732 \times {10^{ - 2}}(\because \sqrt 3 = 1.732)$
Write $1.732 \approx 2$.
$ \Rightarrow {T_{\min }} = 6 \times 2 \times {10^{ - 2}}$
$ = 12 \times {10^{ - 2}}$
$ = 0.12\sec $