
A horizontal force of
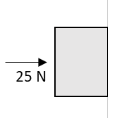
A.
B.
C.
D.

Answer
487.5k+ views
1 likes
Hint:Use the expression for Newton’s second law of motion and also use the formula for static frictional force in terms of coefficient of static friction and normal force. Draw the free body diagram of the block. From this free body diagram first calculate the normal force between the wall and the block. Then apply Newton’s second law in vertical direction and calculate the weight of the block using formula for frictional force.
Formulae used:
The expression for Newton’s second law of motion is
Here,
The static frictional force
Here,
Complete step by step answer:
We have given that the horizontal force required to hold the block in its position on the wall is
We have asked to calculate the weight of the block. Let us draw the free body diagram of the block.
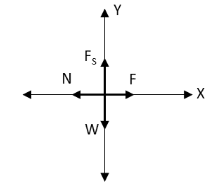
In the above free body diagram,
Substitute
Hence, the normal force exerted by the wall on the block is
Let us now calculate the weight of the block.Apply Newton’s second law of motion to the block in the vertical direction.
Substitute
Substitute
Therefore, the weight of the block is
Hence, the correct option is C.
Note:The students may think that we have applied Newton’s second law of motion to the block in the horizontal and vertical component. But we have not used the right hand side terms in the expression for Newton’s second law. The students should keep in mind that the block is stationary on the wall. Hence, the acceleration of the block is zero. Hence, the net force on the block is also zero. So, the right hand side term in the expression for Newton’ second law is zero.
Formulae used:
The expression for Newton’s second law of motion is
Here,
The static frictional force
Here,
Complete step by step answer:
We have given that the horizontal force required to hold the block in its position on the wall is
We have asked to calculate the weight of the block. Let us draw the free body diagram of the block.

In the above free body diagram,
Substitute
Hence, the normal force exerted by the wall on the block is
Let us now calculate the weight of the block.Apply Newton’s second law of motion to the block in the vertical direction.
Substitute
Substitute
Therefore, the weight of the block is
Hence, the correct option is C.
Note:The students may think that we have applied Newton’s second law of motion to the block in the horizontal and vertical component. But we have not used the right hand side terms in the expression for Newton’s second law. The students should keep in mind that the block is stationary on the wall. Hence, the acceleration of the block is zero. Hence, the net force on the block is also zero. So, the right hand side term in the expression for Newton’ second law is zero.
Recently Updated Pages
Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Trending doubts
Which one is a true fish A Jellyfish B Starfish C Dogfish class 11 biology CBSE

The flightless birds Rhea Kiwi and Emu respectively class 11 biology CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE




